果物をいっぱい食べたい

統計、機械学習周りの勉強や提案やOSS開発の記録

トップ > 因果推論 > 色々なIPWの整理 〜 Stabilized weights の使い所 〜 (2)

色々なIPWの整理 〜 Stabilized weights の使い所 〜 (2)

因果推論 統計学

前回の記事に引き続き、 IPW についての連載第2弾です。

今回も what if book を中心に議論していきます。

目次はこちらです。

IPW や Stabilized weights についての what if book の主張を紹介した後で、Stabilized weights の使い所についていくつかの角度から説明していきます。

記事のゴール

前回の記事では、single time point exposure の条件下での平均因果効果の推定にあたって、以下の2つの主張について説明しました:

  1. IPW によって処置 a' \in \mathcal{A} の Potential outcome \mathbb{E}[Y^{(a')}] を推定するときの基本は、 \mathbb{E} [ \frac{I(A, a')Y}{f_{A \mid L}(a' \mid L)} ] を estimand とした Horvitz-Thompson estimator の推定である
  2. Hajek (modified Horvitz-Thompson) estimator は不偏推定量ではないが、いくつかの仮定のもとで Horvitz-Thompson estimator よりも漸近分散が小さい

本記事では、前回の記事で4つ目の主張として紹介していた以下の内容について説明することをゴールにします:

  • Stabilized weights は Hajek estimator を推定するときに有用かもしれないが、他の推定量を推定するときには注意が必要 (特に、Doubly robust では適切な使用方法がわからない)

Notationは前回の記事を踏襲します。

新規性

新規性が気になる方のために、既存の資料と比較しておきます。

以下の点で新規性があると考えています:

  • IPW において、 stabilized weights を使うことが妥当と思われる条件を調べ、 stabilized weights の安易な利用に警鐘をならした
  • what if book における IPW と exchangeability と stabilized weights の関係性の不明点を列挙した（列挙しただけ）
  • Doubly robust 推定量において stabilized weights を使うべきではないということを理論的な背景から説明した

前提知識

前回の記事 (1) の Notation と、 Horvitz-Thompson estimator と Hajek estimator の定義を理解していることを前提知識にします。

IPWの目的

Stabilized weights を理解するには、「逆確率で重みづけすることの意味や目的」について整理する必要があると考えているので、その部分の説明から始めます。

what if book の2章の紹介

前回の記事でも軽く触れたのですが、 IPW の目的は「データを augmentation することによって、exchangeability が成立するような擬似データセットを作ること」と言えます。

この件について、以前勉強会で私が発表を行ったときに、「IPW はピコ太郎だ」という旨のスライドを作成しました:

f:id:fullflu:20200509145955p:plain
IPWがデータを augmentation していることの直感的な説明

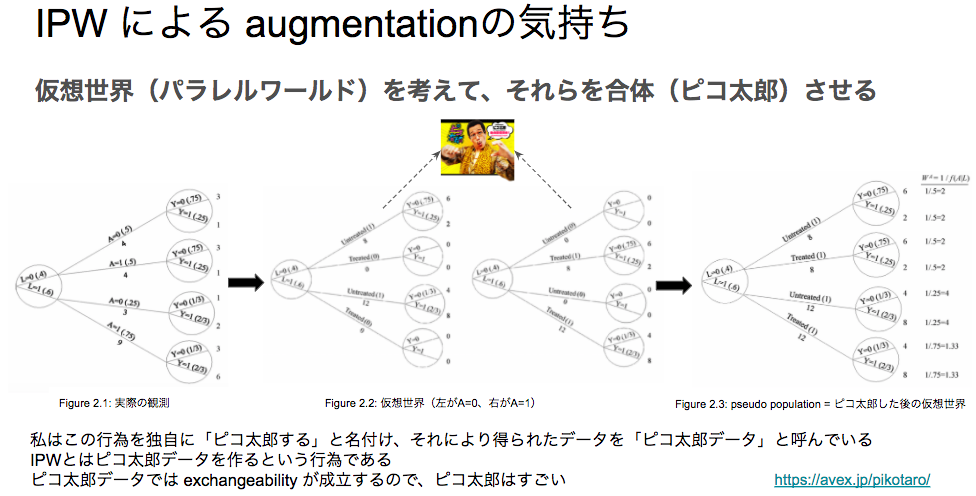
スライドに掲載している図はすべて what if book の2章から拾ってきている*1のですが、「介入が行われた世界線と、行われなかった世界線を考えて、それらを（ピコ太郎のように）合体させた pseudo population（擬似データセット） を作ること」を IPW の目的だと主張するものです。

逆確率を用いてサンプルを重みづけすれば、そのような擬似データセットを作成することができます。

擬似データセットの特徴としては、 what if book の Figure 2.3 の手前で以下のように述べられています:

Under conditional exchangeability in the original population, the treated and the untreated are (unconditionally) exchangeable in the pseudo-population because the L is independent of A

つまり、共変量と処置が独立になり、（条件づきではない）exchangeability が成立するということです。

そして、以下の文が続きます:

That is, the associational risk ratio in the pseudo-population is equal to the causal risk ratio in both the pseudo-population and the original population

exchangeability が成立することで、擬似データにおける関連のリスク比と、擬似データにおける因果のリスク比と、元のデータにおける因果のリスク比がすべて一致すると述べられています。

なお、処置が二値の場合、因果のリスク比は以下のように定義されます:

\begin{eqnarray} \frac{\mathbb{E}[Y^{a=1}] }{ \mathbb{E}[Y^{a=0}] } \tag{1} \end{eqnarray}

さらに、 Technical Point 2.3 では、逆確率を用いて擬似データセットを作ることで、リスク比が一致するだけでなく、 Potential outcome の期待値についての以下の等式も成立することが示されています:

\begin{eqnarray} \mathbb{E}[Y^{(a')}] = \mathbb{E} \Bigl[ \frac{I(A, a')Y}{f_{A \mid L}(a' \mid L)} \Bigr] \tag{2} \end{eqnarray}

この等式が成立することから、因果のリスク比が関連のリスク比と一致することも自明ですし、因果のリスク差（ATE）が関連のリスク差と一致することも自明なので、 IPW の有用性を感じられるかと思います。

2章の主張への疑問点

先ほど「exchangeability が成立する」と述べましたが、 what if book の中で厳密な証明を発見することができませんでした*2。

ただし、これまでの流れから察するに、共変量と処置の独立性からpseudo-population の世界において確率変数の意味での exchangeability が成立するということは言えるかもしれません。

また、式 (2) によって 「pseudo-populationでの期待値と元のデータのpotential outcomeの期待値が一致する」 という（2つのデータ間のmean exchangeability のような）ことは言えたと思います。

しかし、pseudo-population の世界において確率変数の意味での exchangeability が成立することが何に使えるのか ということは明記されておらず、なぜこのようなことを考えたいのかが不明瞭であるように感じました（Technical Point 2.3が pseudo-population の世界における確率変数の意味での exchangeability とどう結びつくのがわからないです）。

今後この記事の中で何度か exchangeability についての言及を行いますが、このあたりが曖昧なままになっているということを前提にお読みいただけると幸いです。

what if book 12.3 節の紹介

Stabilized weights について最も丁寧に述べている資料は what if book 12.3 節だと思うので、そこで述べられている内容を紹介します。

12.3 節の主張をまとめると「IPW の目的を踏まえると、必ずしも逆確率で重みづけを行わなくてもよい」というものになります。

色々な擬似データセットの生成

12.3節の冒頭では、 IPW の目的が共変量と処置の関連がないような（exchangeabilityが成立するような）擬似データセットの作成だということが再度強調されています。

The goal of IP weighting is to create a pseudo-population in which there is no association between the covariates L and treatment A

そして、逆確率による重みづけは、 そのような特徴を持つデータセットのクラスの中で、元のデータの2倍の大きさの擬似データセットを作成していることになると説明されています:

\begin{eqnarray} \mathbb{E}_{A}\Bigl[\frac{1} { f_{A \mid L}(A \mid L=l) } \Bigr] = \frac{\Pr[A=1 \mid L=l] }{ f_{A \mid L}(1 \mid L=l)} + \frac{ \Pr[A=0 \mid L=l] }{ f_{A \mid L}(0 \mid L=l)} = 2 \tag{3} \end{eqnarray}

しかし、ここで「共変量と処置が独立になるような擬似データセットを作る方法は他にもある」という主張がされています:

However, there are other ways to create a pseudo-population in which L and A are independent.

その直後に直感的な説明として、「逆確率に一律 0.5 をかけたもので重みづけをしても、 exchangeability への影響はなくて、かつ擬似データセットのサイズは元のデータと同じになる」という主張がされています。

詳しくは、擬似データセットについての定理により正当化されています。

擬似データセットについての定理

Technical Point 12.2 では、任意の関数 g(A) （正の値をとる必要がある）を使って重みづけを行うことに妥当性があるということを、Estimand が Potential outcome の期待値と等しくなる式によって説明しています。

すなわち、以下が成立することをもって、どんな関数を使っても妥当だという話になっています。

\begin{eqnarray} \frac{\mathbb{E} \Bigl[ \frac{I(A, a')Y}{f_{A \mid L}(a' \mid L)} g(A) \Bigr]} {\mathbb{E} \Bigl[ \frac{I(A, a')}{f_{A \mid L}(a' \mid L)} g(A) \Bigr]} &=& \frac{\mathbb{E}[Y^{(a')}] g(a')} {g(a')} \\ &=& \mathbb{E}[Y^{(a')}] \tag{4} \end{eqnarray}

どの関数を使うべきか

関数 g として、処置の確率 f_A(a') ないしはその推定結果を使うべきだという主張がされています。

このとき、実際の推定は以下のように行われます:

\begin{eqnarray} \frac{\sum_{i=1}^{n} \Bigl[ \frac{\hat{f}(A_i)}{\hat{f}_{A \mid L}(A_i \mid L_i)}I(A_i, a')Y_i \Bigr]} {\sum_{i=1}^{n} \Bigl[ \frac{\hat{f}(A_i)}{\hat{f}_{A \mid L}(A_i \mid L_i)} I(A_i, a')\Bigr]} \tag{5} \end{eqnarray}

ここで使われた重みのことを stabilized weights と定義しています。

Stabilized weights を使うべき理由として、 Estimand が変わらないという条件を満たしつつ、一定の条件のもとで信頼区間が小さくなることを挙げられています。

また、effect modifier が存在するときは、effect modifier で条件づけた処置確率の推定結果を使うことが良しとされています。

what if book 12.3 節の補足と修正提案

以上をご覧になった方は、stabilized weights は素晴らしいもので、 IPW を考えるときにはなんでもかんでも stabilized weights を使えばいいような気持ちになるかもしれません。

しかし、ここから先では、 stabilized weights をそのまま使うと誤った解釈に至りうるケースについての指摘を行おうと思います。

ここでの結論は以下のようになります:

  • Technical Point 12.2 は Hajek estimator を Estimand にした場合の話であり、それ以外の推定量について同様の等式が成り立つという保証はないのでは？
  • 例えば、 Horvitz-Thompson estimator を Estimand にしたときは補正が必要になる（というかそもそも Horvitz-Thompson estimator で stabilized weights を使っても意味がない）のでは？

擬似データセットについての定理の補足

Technical Point 12.2 では、 Estimand が Potential outcome の期待値と等しくなる式を紹介しています。

しかし、前回の記事を読んでいただいた方はわかると思うのですが、これは Hajek estimator を Estimand とした場合の式展開になります。

Horvitz-Thompson estimator を Estimand にしたときは以下のように計算できます:

\begin{eqnarray} \mathbb{E} \Bigl[ \frac{I(A, a')Y}{f_{A \mid L}(a' \mid L)} g(A) \Bigr] &=& \mathbb{E}[Y^{(a')}] g(a') \\ \tag{6} \end{eqnarray}

つまり、stabilized weights を使った場合、 g(a') の逆数をかける必要が出てきます。

ただし、式を見るとわかるように、計算結果全体に対して g(a') を一律でかけただけになっているので、そもそもこの場合は stabilized weights を使う意味がありません。

このように、なんでもかんでも stabilized weights を使うべきとは言えない上に、誤った使い方をすると推定結果がおかしな値になってしまう可能性があります。

Technical Point 12.2 ではこうした前提条件が明示的に記述されていなかったため、誤った使い方をしてしまうリスクが一定存在すると考えられ、本記事で補足を行う価値があると判断しました*3。

Technical Point 12.2 以外の記述について

Stabilized weights を使うことの妥当性が Technical Point 12.2 に依存しているのであれば、 12.3 節の中で直感的な説明を行う部分についても、Technical Point 12.2 の前提条件（Hajek estimator の推定であること）を明示した方がよいと考えています*4。

逆にいうと、「他の推定量を扱う場合に、stabilized weights を使うことの妥当性がどのような直感で説明されるのか」という説明があるとより親切だと感じました*5。

また、 Hajek estimator を紹介するときに、 「重みづけするweight のスケーリングに対して、少なくとも Estimand の世界では計算結果が不変*6」といった特徴を記載してもよいのではないかと感じました。

Doubly robust 推定量と 様々な IPW 推定量

IPW を使った手法として、Doubly robust という便利なものが知られています。

記事の締めくくりとして、 Doubly robust 推定量 と 様々な IPW 推定量の関係性についての私見を述べます。

結論としては、以下になります:

  • Horvitz-Thompson estimator 以外の IPW 推定量を Doubly robust で使うのは難しい（方法がわからない）
  • 例えば、 Stabilized weights をむやみに Doubly robust で使うのは危険

Doubly robust 推定量

IPW では、傾向スコアモデルが正しく推定されていた場合、因果効果の推定結果にバイアスがのらないという保証はできません。

また、アウトカム回帰モデルを利用した Standardization*7 では、回帰モデルが誤って推定されていた場合、因果効果の推定結果にバイアスがのらないという保証はできません。

そこで、「傾向スコアモデルかアウトカム回帰モデルの少なくとも一方が正しく推定されていれば因果効果の推定結果にバイアスがのらないような推定量」として Doubly robust 推定量が提案されています*8。

処置が二値のとき、処置 a' の Potential outcome の期待値の Doubly robust 推定量は以下のように定義できます:

\begin{eqnarray} \hat{\mathbb{E}}_{DR}[Y^{(a')}] &:=& \frac{1}{n} \sum_{i=1}^{n}\Bigl[\frac{I(A_i, a')Y_i}{\hat{f}_{A \mid L}(a' \mid L_i)} + \Bigl(1 - \frac{I(A_i, a')}{\hat{f}_{A \mid L}(a' \mid L_i)}\Bigr) \hat{f}_{Y\mid A, L}(a', L_i)\Bigr] \tag{7} \end{eqnarray}

what if book では Technical Point 13.2 で紹介されており、 Horvitz-Thompson estimator を アウトカム回帰モデルを伴った関数で補正しているとみなせます:

which can also be viewed as a correction of the Horvitz-Thompson estimator by a function that involves the outcome regression model

式を見ると明らかですが、 summation の中身の一項目は Horvitz-Thompson estimator と同じ形をしています。

また、二項目において、 Standardization を傾向スコアにより補正しています。

要するに、IPW と Standardization の合わせ技が Doubly robust ということになります。

Horvitz-Thompson estimator 以外の IPW 推定量を Doubly robust で使えるか？

さて、IPW を学んできた立場としては、以下のことが気になるのは自然なことかと思います:

  • Doubly robust で、 Stabilized weights は使えるのか？
  • Doubly robust で、 Horvitz-Thompson estimator 以外の形の推定量も使えるのか？

これについて説明した資料はなかなか見つけられなかったのですが、私の意見は「自明ではなく、難しそう」です。

いくつかの具体例をもとに考察していきます。

例えば、stabilized weights を 式 (7) に導入する方法についていくつか考えてみます。

まず、逆確率の部分を直接処置確率で補正すると、このようになると思います:

\begin{eqnarray} \frac{1}{n} \sum_{i=1}^{n}\Bigl[\frac{I(A_i, a')\hat{f}_{A}(a')Y_i}{\hat{f}_{A \mid L}(a' \mid L_i)} + \Bigl(1 - \frac{I(A_i, a') \hat{f}_{A}(a') }{\hat{f}_{A \mid L}(a' \mid L_i)}\Bigr) \hat{f}_{Y\mid A, L}(a', L_i)\Bigr] \tag{8} \end{eqnarray}

しかしこの式は、「傾向スコアモデルが正しく推定できているがアウトカムモデルが誤って推定されている」ときにバイアスが生じてしまうので、 Doubly robust とは言えません。

また、式全体に対して処置確率で補正をするとこのようになります。

\begin{eqnarray} \frac{1}{n} \sum_{i=1}^{n}\Bigl[\frac{I(A_i, a')\hat{f}_{A}(a')Y_i}{\hat{f}_{A \mid L}(a' \mid L_i)} + \hat{f}_{A}(a') \Bigl(1 - \frac{I(A_i, a') }{\hat{f}_{A \mid L}(a' \mid L_i)}\Bigr) \hat{f}_{Y\mid A, L}(a', L_i)\Bigr] \tag{9} \end{eqnarray}

しかしこの式は、「傾向スコアモデルが誤って推定されているがアウトカムモデルが正しく推定されている」ときにバイアスが生じてしまう上、全体に処置確率をかけているだけなので、 Doubly robust でない上に stabilization の意味もありません。

また、 summation の中身の一項目（Horvitz-Thompson estimator）、あるいは 二項目（Standardization の補正）のどちらか一方にのみ補正を行う場合、色々なケースで明らかにバイアスが出てきてしまうので不適切です。

よって、 Doubly robust で Horvitz-Thompson estimator を扱う場合、 Stabilized weights を使うことは難しいと考えられます。

最後に、Doubly robust で Hajek estimator のようなものを扱う場合を考えてみます。

この記事の前半で述べたように、 Stabilized weights の有用性は Hajek estimator を扱うときに発揮されるので、 Doubly robust でも Hajek estimator のようなものを考えれば Stabilized weights を使えるかもしれないという発想に至るでしょう。

素朴に考えると、以下のように分母をつけたくなるかと思います。

\begin{eqnarray} \frac{ \sum_{i=1}^{n}\Bigl[\frac{I(A_i, a')Y_i}{\hat{f}_{A \mid L}(a' \mid L_i)} + \Bigl(1 - \frac{I(A_i, a')}{\hat{f}_{A \mid L}(a' \mid L_i)}\Bigr) \hat{f}_{Y\mid A, L}(a', L_i)\Bigr] } { \sum_{i=1}^{n} \Bigl[ \frac{I(A_i, a')}{\hat{f}_{A_i \mid L}(a' \mid L_i)} \Bigr] } \tag{10} \end{eqnarray}

しかし、前回の記事で指摘したように、これは ratio estimator の特殊ケースなので、傾向スコアモデルが正しく推定されていたとしても、不偏性は持たないというのが私の意見です。

またそもそも、傾向スコアモデルが誤って推定されていたとき、分母の期待値は n とは大きく異なることが予想されるので、式 (10) は傾向スコアモデルに対してロバストではない（すなわち、 Doubly robust ではない）推定量と言えるかと思います。

よって、 Hajek estimator のような形の Doubly robust 推定量を作ることは難しく、式 (10) に対する stabilized weights を考えるまでもなくお蔵入りになってしまうでしょう。

まとめ

本記事では、 IPW の文脈でよく紹介される stabilized weights という重みづけ方法の特徴と、その注意点をまとめました。

一通り読んでいただいた方には、「なんでもかんでも stabilized weights を使えばいい」というわけではないことがお伝えできたかと思います。

今後は、より一般的な連続値の介入を想定した手法や、実験による主張の検証についての記事を書く予定をしています。

記事を読んでいただいた皆さんの豊かな因果推論ライフに貢献できれば幸いです。

*1:もちろんピコ太郎氏の写真は what if book には載っていません。Avex さんの HP (https://avex.jp/pikotaro/) から借りてきました

*2:ご存知の方は教えていただけると幸いです

*3:Technical Point 12.1 で「この章では Hajek esitmator を推定する」とは書かれていますが、これが stabilized weights を使うにあたっての本質的な前提条件であることに気付いている読者は多くはないと思います・・・

*4:これは先ほどの「pseudo-population の世界において確率変数の意味での exchangeability が成立することが何に使えるのかわからない」という疑問とも関連していて、pseudo-population の世界において確率変数の意味での exchangeability が成立するような stabilized weights を使ったとしても、結局は別の基準（不偏性や漸近分散）をもとに議論するのであれば、pseudo-population における exchangeability とはいったい何なんだろう・・・という気持ちになりました

*5:私も適切な説明はまだ思いついていないです

*6:「不偏」の間違いではなく invariant の意味です

*7:g-formula として what if book の 13章で紹介されています

*8:この記事では議論を簡略化するために「真の関数が得られている」という意味での「正しく推定されている」という条件下での不遍性を考えました。しかし、Doubly robust 推定量の性質を語るときには、モデルが特定されている」という条件下での漸近的な不偏性（これを一致性と呼んでいる文献もある気がします）を持つものとしての議論をすることが多いと思われます。適宜読み替えていただけると幸いです