【書評/書籍紹介】施策デザインのための機械学習入門 〜データ分析技術のビジネス活用における正しい考え方
本記事では、2021年8月4日に技術評論社さまから発売された施策デザインのための機械学習入門〜データ分析技術のビジネス活用における正しい考え方（齋藤優太、安井翔太 著、株式会社ホクソエム 監修; 以下本書と呼びます）の紹介を行います。
なお、本書の詳しい内容や執筆背景については著者がすでにブログを書かれているので、まずは著者の記事をご覧になった上で、一読者の感想として私の書評記事を読んでいただければと思います。
紹介の経緯
以前からお世話になっていた著者の齋藤(@usait0)さんからありがたいことに電子版の献本をしていただき、お盆休みの数日を使い読ませていただきました。
献本への感謝の気持ちに加え、本書に内容を十分に理解した上で一緒にデータ分析の施策デザインの質を高めていく仲間が増えると私自身もハッピーになりそうな予感を強く感じたため、一人でもそのような仲間を増やせるとよいなという気持ちで記事を書くことにしました。本書が指南書・啓蒙書という形をとっていることにあやかり、本記事もそれに乗っかった形をとろうと思います。
自分で本記事を読み返してみると、「全体的にベタ褒めしすぎでは？」「記事の書き方が冗長すぎでは？」という印象を持たれそうな気がしましたが、心の赴くままに書いた結果なのでご容赦いただければと思います。
本書の目次
目次は以下のようになっています:
1章 機械学習実践のためのフレームワーク 2章 機械学習実践のための基礎技術 3章 Explicit Feedbackを用いた推薦システム構築の実践 4章 Implicit Feedbackを用いた推薦システムの構築 5章 因果効果を考慮したランキングシステムの構築 付録A 演習問題
詳細はHPで確認していただければと思いますが、個人的には、1章と2章が良い意味で期待を裏切られる内容でした。
章の粒度でタイトルだけを見ると「1-2章では 機械学習とは〜〜 のようなふわっとした話が展開されるのかな？」という気がしなくもないですが、非常にしっかりとした内容で、むしろこの2つの章が本書の根幹になる部分だと感じました（IPWLearnerでOff Policy Learningを行うという、知名度は低いが本書の根幹となる重要な手法もここで紹介されています）。
それに伴い、本書の読み方としては、1章から順に読んでいき、後半の具体例を眺めることで、自分の普段向き合っているビジネス課題との対応を考えながら進めていくというやり方が適切そうだと感じました。
対象読者
はじめに の章によると、本書のターゲットは
だと記載されています。ここで最も重要なのは すべての という部分で、特定の機械学習のタスク・技術にフォーカスした内容ではなく、ほとんどすべての機械学習施策で共通して役に立つ内容を扱っている点だと考えます。読者が解いているタスクがユーザのデモグラ予測だろうがアイテムの推薦や並び替えであろうが、またそのために使う手法が勾配ブースティングだろうが深層学習であろうが（なんならルールベースであろうが）、本書のフレームワークや思考方法を活用することで施策の質を高めてくれる可能性があるでしょう。
その理由は、本書が「機械学習を機能させるために、どのようなステップが必要であるか」を言語化した上で、現実に起こりうる様々なビジネス課題に対して、「どのように解くか」ではなく「何を解くか」を上流部分から定式化していくスタンスをとっていることにあると考えます。これについての詳細は後で説明します。
私個人の感想としては、すべての という表現は誇張ではないものの、読者の背景に合わせて訴求ポイントは変わりそうだと感じました。具体的には以下の3つのパターンを想定し、それぞれのパターンに対する訴求ポイントを、本書の内容について触れながら説明していこうと思います:
- 「目次に出てくる 機械学習実践に潜む落とし穴 や バイアス や 反実仮想機械学習 に興味があり、ちゃんと勉強してみたい」と思っている人
- 「データ分析において 何を解くか を考えるのが元々得意だし、反実仮想機械学習 のことも知ってる。でも結局この話はケースバイケースなので、わざわざ本書を買う必要はなさそう」と感じている人
- 「普段機械学習をやっているが、詳細目次に出てくる 反実仮想機械学習 といった専門用語がピンとこないので買うか迷っている」人
訴求ポイント:
- ご興味にぴったりの本だと思うので、マストバイだと思います。
- 私の知る限りですが、 何を解くか を考えて定式化するという文脈において、本書以上に整理された資料や議論は存在しないです。ある程度自信のある人であっても、本書を活用することでより思考の質を高められると考えます（私自身、著者が公開されているスライドや論文の大部分には元々目を通していましたが、それでもなお多くの学びがありました）。
- 本書の本質は 反実仮想機械学習 という方法論ではなく、 何を解くか を定式化する部分にあると思うので、その部分に興味がある場合はおすすめできます。また、 反実仮想機械学習 自体がここ5年くらいのトレンドなので、分野として追い始めるきっかけに使うという手もありそうです。
ちなみに、2021年8月13日時点でAmazonの情報学・情報科学全般関連書籍カテゴリーの中でベストセラー1位だったので、すでにかなり多くの方が購入されていると推測され、この記事の存在価値は書き始める前からすでに危ういです（書評記事に仲間集めの方向性を強めに置いたのはそれも理由の一つです）。
対象でない読者
個人の感想としては、「データ分析に関わるビジネス課題の 定式化 に興味がない人」は対象外かなと感じました。
特定の機械学習手法の研究者でそのクオリティを高めていきたい方や、あるいは分析プロジェクトに企画職として関わる方の中には、これに該当する方がいらっしゃるかと思います。
判断が難しいのは、本書の概要だけを理解して 何を解くか について専門家と議論をしていきたい企画職の方でしょうか。本書では、想定知識としては統計学や機械学習の基礎知識を仮定されています。機械学習の 損失関数の最小化 を中心としたアプローチに慣れていない方が本書に対してどのような印象を持つかはわからないですが、そこは我々専門家がコミュニケーションしながら個別に期待値調整をする必要があるかな、というのが私の感想です。
本の中身
本書を読んだ中で個人的に重要だと感じた点を列挙します:
- ビジネス課題に対して「何を解くか」を、上流部分から定式化しているところ
- ビジネス課題を解く際に有用な思考フレームワークを定義し、そのフレームワークに沿った議論が一貫してなされているところ
- 一つの定式化や手法を正解として与えるわけではなく、試行錯誤を通してより良い定式化に辿り着くための実務家向け指南書としての側面が強調されているところ
- 反実仮想機械学習（CFML）の手法を丁寧に解説しているところ
- データやコードがすべて公開されており、実際に使ってみるハードルが低いところ
4と5 は議論の余地が少なそうなので、それ以外について以下で詳細に補足します。ただし、ここから先は未読者への紹介というよりは、既読者とのコミュニケーションと自己満足の側面が強くなっていきます。
定式化
対象読者のところでもお話しましたが、本書は「機械学習を機能させるために、どのようなステップが必要であるか」を言語化した上で、現実に起こりうる様々なビジネス課題に対して、「どのように解くか」ではなく「何を解くか」を上流部分から定式化していくという点で、他の本にない独自の価値を持っています。
ここで注目すべきは 定式化 という部分です。
世の中には「モデルの性能を追い求める前に、どういう問題を解くかを設計することが重要だ」ということを語る方は多く存在していますが、「具体的にどのような思考のフレームを使えばそのクオリティを高めていけるのか」という問いに対して明確な回答を持っている方を私はこれまで観測したことがありませんでした。私自身もそうだったのですが、このような議論は結局ケースバイケースになってしまい、「具体と抽象の間をうまく行き来しながらちょうど良い解像度で何を解くかを語ることは非常に難しいよね」というある種の諦めを持っている方は多いのではないでしょうか。
本書はこれに対し、実例をベースに「悪い問いの立て方」と「良い問いの立て方」の違いを数式の世界で表現しています。1章を読んだ時点で、定式化 についてのこれまでの認識を一歩前に進める世界観を提示しているような感想を抱きました。
具体例を挙げすぎるとネタバレになってしまうので難しいのですが、Xという属性の人の値Yを関数fで予測して損失関数lで評価したくなるであろうケースにおいて、
]
を解くべき問題としていいんだっけ？それって観測データで素朴に経験近似していいんだっけ？のような話を突き詰めていく感覚です。
フレームワーク
本書では、ビジネス課題を解くにあたって独自の思考フレームワークを導入し、そのフレームワークに基づいて一貫して議論が展開されています。以下の目次からなる 1.2 機械学習実践のためのフレームワーク で提案されている6段階からなるフレームワークです:
1.2.1 KPIを設定する 1.2.2 データの観測構造をモデル化する 1.2.3 解くべき問題を特定する 1.2.4 観測データを用いて解くべき問題を近似する 1.2.5 機械学習モデルを学習する 1.2.6 施策を導入する
データ分析のフレームワークというと、多くの方が第一に思い浮かべるのは CRISP-DM だと思います。私自身CRISP-DMのフレームワークに従って問題を考えることは多いですし、CRISP-DM自体の有用さは間違いないと思います。しかし、CRISP-DMだけでは、より良い定式化をするためのヒントを得ることは難しいと感じていました。参考のため、本書とCRISP-DMの対応を考えてみます。
1.2.1 KPIを設定する は、Business Understandingに対応しそうです。
1.2.2 データの観測構造をモデル化する は、Data Understanding に対応しそうです。ただし、CRISP-DMではこのステップでは可視化やEDAがメインになることが多いですが、本書ではデータ生成過程を式で表現するところがメインになります。CRISP-DMの Data Understanding では「生成過程を式で書くこと」を明言されていなかったという認識をしており、実際の業務の場でも、生成過程をしっかりと式で書き切っているケースばかりではないでしょう。本書はその部分を明示的に書いている、という点が重要な違いの一つだと感じました。
1.2.3 解くべき問題を特定する・ 1.2.4 観測データを用いて解くべき問題を近似する・1.2.5 機械学習モデルを学習する は Modeling・Evaluation に対応します。この部分の具体性の違いも重要な部分だと感じました。CRISP-DMでは、各ステップについてそこまで踏み込んだ議論はされていない認識です。一方本書では、「解くべき問題を間違えるとどうなるのか」について例示し、このステップの解像度を高めています。また、「解くべき問題の特定と観測データを使った近似の間にギャップが存在しうる」という点に注目し、その二つのステップを明確に分離しています。モデルの学習や評価においても、学習したモデルの評価を事前に行うOff Policy Evaluationという仕組みを詳しく説明しているという点で、CRISP-DMよりは厳密な評価を想定していると言えるでしょう。
最後の 1.2.6 施策を導入する は Deployment に対応しています。本書のユニークな特徴として、「施策の導入によって将来のデータが生成される」という点に着目し、MLOpsの文脈では語られることがほとんどない「将来のモデル改善のためのデータ生成装置としての機械学習モデルの導入」を実践しているところが挙げられるでしょう。
一方、CRISP-DMの Data Preparation に当たる内容は本書では明確に述べられていません。 1.2.5 機械学習モデルを学習する の中にデータを準備する工程も含まれていそうですが、前処理や特徴量設計については詳しい書籍が既に多く存在しているため、本書はその詳細については触れないというスタンスをとっているようでした。本書でも繰り返し述べられていますが、特定のフレームワークを絶対視することなく、目的に応じて適宜チューニングしていく姿勢が重要になります。いずれにせよ、思考を整理してくれる良質なフレームワークが増えるに越したことはないので、分析者にとって助けになる内容だと感じました。
試行錯誤・実務家向け指南書
本書の大きな特徴として、特定のフレームワークや手法を絶対視せずに、目的に応じてチューニングしていくことを何度も強調されている点が挙げられます。その上で、実務家が自分で応用できる力を養成すべく、「素朴に定式化したらどうなるか」「それでどういう問題が発生するか」「改善するためにはどうすればいいか」という流れで説明がなされています。
冒頭で述べた通り、何を解くか というテーマの議論は非常に難しくケースバイケースであるので、この点を強調されているのは非常にありがたいです。実際私も、本書を読んだことをきっかけに普段の定式化行動を省みてみましたが、反省すべき点や改善すべき点が多々存在していました。また、本書の内容をさらに進めて「こういうことも考えられそうだな」という案もいくつか出てきました。
全部の案は書ききれないので、参考までに私の思考の一部を以下で掲載しておきます。
2.2のcolumn
ログデータを収集した際に稼働していた意思決定モデルが行動選択に用いた特徴量を分析者がすべて把握していること という仮定が紹介されており、ビジネス現場ではその仮定は満たされることが多いと述べられていました。私の解釈では、この仮定はoutcome regression modelの交絡を防ぐためだと考えています（IPS推定量については処置確率だけわかっていればよい）。そして、outcome regression modelを作る場合には、過去施策の特徴量を把握しているだけではなく、過去施策の特徴量をすべて使って交絡を調整することまでが必要になるように思えました。これが何を意味しているかというと、「outcome regression modelを使ってモデル改善をする前提では、モデルがupdateされるたびに考慮するべき特徴量が増えていく」ということであり、「無闇矢鱈にモデルに使う特徴量を増やすと後々のモデル改善が大変になりかねない」というメッセージに繋がりそうだなと感じました。
Off Policy Evaluationとモデル選択
本書ではOff Policy Evaluation (OPE) によってモデルの性能を評価し、より良いモデルを選択するという手続きが説明されています。これについて、本書の思考に則ると、「より良いモデルを選択する ことがやりたいのであれば、 モデルの性能の評価 は解きたい問題と違うタスクを解いていることになるのではないか」という疑問を抱くのが自然かと思います。
この点について本書の著者に質問してみたところ、 Confident Off-Policy Evaluation and Selection through Self-Normalized Importance Weighting という論文がAISTATS 2021で発表されており、そのような疑問を解決していく方向性も存在しているようでした。自分がゼロから理論を組み立てるのはなかなか大変そうですが、参考にできるところを取り入れながら業務に応用していきたいところです。
regression-EM周り
regression-EMについて、著者が以前以下の疑問を書かれていました:
regression-EMでやっているrelevanceパラメータをGBDTで予測するパートだけど, それがそもそもUnbiased LTRでやりたいことなので, regression-EMのアルゴリズムで精度よくpropensity推定できるならそもそもpropensity推定のこと考える必要ないのでは？という本末転倒な感じがした...
本書にはこの疑問点についての言及は存在していなかったのですが、私自身regression-EMの論文を読んだときに同じような感想を持っていました。しかし、本書の思考をトレースしてみると、この2段階のアプローチをとっている理由は、最終的に解くべき問題に対して改めてチューニングするためなのかなという仮説に至りました。多少粗くてもいいいのでポジションバイアスを推定してくれれば、あとは後段の学習でなんとかするという気持ちがあるのかもしれないです。これについては、本書で紹介されているポジションバイアス推定の後続研究を読んでいくと何かしらのヒントが得られるかもしれないです。
おわりに
以上で紹介は終わりです。
改めてではありますが、献本していただいた齋藤(@usait0)さん、ならびに執筆に関わられたみなさま、ありがとうございました。
同じような問題に興味を持たれた方と、本書をもとに議論やお仕事をする機会があれば嬉しいなと思っております。
g-estimation を推定方程式で定式化するまでの行間を埋めてみる
本記事では、 g-estimation でパラメータ推定を行う際に推定方程式を用いる方法について説明します。what if book の14章で紹介されている話の一部を深く掘り下げていきます。
記事のゴール
以下の疑問に答えることをゴールにします（what if 勉強会でも疑問として紹介されていました）:
- what if book の本文で紹介されているロジットモデルの係数検定の話と、Technical Point 14.2 で紹介されている推定方程式の話が等価になる理由がわからない
- なぜ推定方程式の形で表現したいのかわからない
執筆終了時点での私の回答としては以下になります:
- 「
と
の相関がないような制約をかけたい」 という気持ちを共分散がゼロになるという式で表現して経験近似するとそうなるから
- (a) 「処置モデルの係数の検定」という制約に縛られる必要がなくなり、処置モデルについてより柔軟なケースを扱えるから (b) 推定方程式の一般論を用いて、推定量の漸近的な性質について語れるから
新規性
- g-estimation と推定方程式の関係性を日本語で一つ一つ解説している記事は見つけられませんでしたので、それを新規性とさせていただきます（正確性は保証できないです）。
前提知識
- what if book の14章に軽く目を通していること（rank preservation, conditional exchangeability, consistency などは記事の中で説明しないです）
- 共分散や検定論といった基本的な統計の概念がわかっていること
what if book の g-estimation のおさらい
what if book 14章では、 g-estimation の定義はふわっとしか与えられていない認識です。
章の構成としては、ざっくり以下のようになっています:
- structural nested mean model (SMM) について導入する
- rank preservation 仮定を紹介する*1
- rank preservation と conditional exchangeability と consistency が成立していたと仮定すると、処置モデルの係数の検定結果によって因果効果を推定できることを示す
- こうした推定のための手続きを g-estimation と呼んでいる
ひとまずは、SMM のパラメータ推定を行うためのトリッキーな手法なんだ、くらいに思っていただけるとよいと思います。
以下、記事のゴールに対して必要最低限と思われる範囲で、 g-estimation の説明を行います。
SMMの導入
SMMは、potential outcome の差分の期待値をモデリングする手法のことを指します。
例えば、以下のようなモデルを立てて、パラメータ を平均因果効果として推定することが目標になります:
\begin{eqnarray}
\mathbb{E}[Y^{a} - Y^{a=0} \mid L] = \beta_1 a
\end{eqnarray}
rank preservation と conditional exchangeability の仮定のもとで、potential outcome の差分が以下のような effect modification のない線形モデルで表現できると仮定します:
\begin{eqnarray}
Y^{a} = Y^{a=0} + \psi_1 a \tag{1}
\end{eqnarray}
なお、rank preservation の仮定によって となりますので、以降はパラメータ
を求めることにフォーカスして考えます。
g-estimation
g-estimation の一歩目として、consistency の仮定から、観測データを用いて式(1)を書き換えます:
\begin{eqnarray}
Y^{a=0} = Y - \psi_1 A \tag{2}
\end{eqnarray}
次に、この式をもう少し抽象化して考えます。
まず、 とすると、真の
に対して
になることは定義より自明です。
また、 conditional exchangeability の仮定により、 と
は
を与えたときに独立になります。
よって、真の に対して
と
は
を与えたときに独立になります。
逆に言えば、 を色々入れ替えながら「
と
が
に対して条件つき独立になるような
を見つけられれば、
それが真の
の候補になる（必要条件）」ことがわかります。
さらに、処置モデルがロジットモデルで特定できていると仮定すると、この条件つき独立性が成り立つとき、 についての係数
がゼロになります。処置モデルの例は以下です:
\begin{eqnarray}
logit(\Pr[A=1 \mid H(\psi), L]) = \alpha_0 + \alpha_1H(\psi) + \alpha_2L \tag{3}
\end{eqnarray}
すなわち、以下の手順で因果効果の候補を推定します:
として色々な値を用意する
- それぞれの値に対して式(3)のモデルを学習させ、係数
が0であるという帰無仮説を検定する
- 検定結果が有意にならなかった
実装時には計算機のパワーでグリッドサーチすることが多いです。
Technical Point 14.2: 推定方程式の紹介
簡単のため、censoringは無視して考えます。
Technical Point 14.2 では、以下の式(4)の推定方程式の解を求めることと、14章でやってきた g-estimation の手続きは等価だと述べられています:
\begin{eqnarray}
\sum_{i=1}^{n} H_i(\psi) (A_i - \mathbb{E}[A \mid L_i]) \tag{4}
\end{eqnarray}
ここで、 はi番目のサンプルの観測値によって計算された
の値です。
期待値の部分は処置モデルを推定して予測すればよいようです。
なぜ推定方程式が出てくるのか
ここからが本記事の本題です。
式の導出
とは言っても考え方は非常にシンプルで、処置のロジットモデルのことは忘れて、「 と
が独立になるような
を求めたい」という原点に立ち帰ればよいです。
この独立性の条件を必要条件に緩めると 「 と
が無相関になるような
を求めたい」になり、その条件を満たす
の集合が解候補になると言えます。
無相関ということは相関係数がゼロということであり、すなわち共分散がゼロということになります。
と
の共分散がゼロであることは、以下の式(5)で表現できます。
\begin{eqnarray}
\mathbb{E}
\biggl[
\bigl( H(\psi) - \mathbb{E}[H(\psi)\mid L]\bigr)
\bigl( A - \mathbb{E}[A \mid L] \bigr)
\biggr]
&=&
\mathbb{E}
\biggl[
H(\psi)
\bigl( A - \mathbb{E}[A \mid L] \bigr)
\biggr] \\
&=& 0 \tag{5}
\end{eqnarray}
よって、結論としては、冒頭に書いた通り、「 と
の相関がないような制約をかけたい」 という気持ちを共分散がゼロになるという式で表現して経験近似したら推定方程式(4)が出てきます。
解析解
式(2)の形でモデルを立てていた場合、推定方程式(5)にHの式を代入して移項と四則演算をするだけで、解 を陽に得られることがわかります。
Hajek estimator と似たような形の解になりますね:
\begin{eqnarray}
\hat{\psi} = \frac{\sum_{i=1}^{n} Y_i (A_i - \mathbb{E}[A \mid L_i])} {\sum_{i=1}^{n} A_i (A_i - \mathbb{E}[A \mid L_i])} \tag{6}
\end{eqnarray}
推定方程式として扱うことの嬉しさ
推定方程式では、ロジットモデルの係数というものを考えていないので、処置モデルの形状については明らかにagnosticです。
よって、推定方程式の形で議論することにより、現実にあったより柔軟なモデルを扱うことが可能、というメリットがあると考えます。
また、Technical Point 14.2 のように、censoringを考慮した定式化にも容易に拡張できたり、
推定方程式の の部分を
] によって置き換えることで doubly robust な推定結果を得られたりするようです（証明は読んでいません）。
このあたりは、推定方程式として定式化したことにより、推定量の性質について語れる部分が増えるというメリットを得たのだと解釈しています。
おわりに
以上、本記事では g-estimation を推定方程式として定式化するまでの行間を埋めて、その意義について考察してきました。
皆さまの疑問点の解消のお役に立てれば幸いです。
誤りがありましたら、そっとご指摘いただけると助かります。
*1:実際の推定では平均因果効果を知りたいだけなので、この仮定は必要ではないですが、思考の過程で便利なので導入しています
Marginal Structural Model のパラメータ推定に重み付き最小二乗法を用いることの正当性
本記事では、 Marginal Structural Model (MSM) のパラメータ推定に重み付き最小二乗法 (IP-Weighted Least Squared method; IP-WLS method) を用いることの正当性についての解釈を試みます。what if book の12章で紹介されている話の一部を深く掘り下げていきます。
- 記事のゴール
- 新規性
- 前提知識
- what if book のMSMのおさらい
- 処置が2値の場合、本当に IP-WLS は Hajek estimator と一致するのか？
- 処置が多値のときはどうなるか？
- M推定量の文脈による正当化（処置が離散の場合）
- M推定量の文脈による正当化（処置が連続の場合）
- おわりに
記事のゴール
以下の3つの問いに答えることを目指します（自分が12章を読んだときに感じた疑問でした）:
- 処置が2値の場合には、IP-WLS の推定量が Hajek estimator と等しいという主張が what if book P152 で書かれているが、これは本当か？
- 処置が多値の場合にも、IP-WLS の推定量は Hajek estimator と等しいのか？
- 処置が連続の場合にも、何かしら似たような解釈はできるのか？
執筆終了時点での私の回答としては以下になります:
- 本当であるということを証明します。
- 星野先生の本の議論を参考にしつつ、等しいことを証明します。
- モーメント法・M推定量の文脈から、自分なりに正当化を試みます。
なお、本記事のタイトルの「正当性」という単語には、
- 特定（処置が離散）の場合に、既知の推定量と同じ結果が得られるという意味で手法の正当化ができる
- 処置が連続の場合も、離散の場合の拡張として捉えると、一定の妥当性があるように思える
といった気持ちを込めています。
新規性
モーメント法・M推定量の文脈で処置が連続の場合のお気持ちを書いてある日本語記事は見つけられませんでしたので、それを新規性とさせていただきます（正確性は保証できないです）。
前提知識
- 過去の自分の記事 における、 Hajek estimator のモーメント法による定式化の雰囲気がわかっていること
what if book のMSMのおさらい
what if book 12章については過去の記事でも紹介しましたが、MSMやそのパラメータ推定方法については述べていなかったので、軽くおさらいします。
モデリング
MSMとは、potential outcome の期待値を（周辺化して）直接予測するようなモデルを立てることを意味します。
過去の記事でも紹介した exchangeability などの仮定のもとで、そのモデルのパラメータの推定結果を用いて因果効果を良い感じに*1推定することが可能です。
処置が2値のとき、以下のような MSM のモデルが 12.4 節で紹介されています:
\begin{eqnarray}
\mathbb{E}[Y^{a}] = \beta_0 + \beta_1 a
\end{eqnarray}
個人的には を使って以下のように書いた方が綺麗だと思うのですが、必要に迫られるまでは慣習にしたがって
を使わずに書きます。
\begin{eqnarray}
\mathbb{E}[Y^{a=a'}] = \beta_0 + \beta_1 a'
\end{eqnarray}
このとき、以下のように因果効果を計算できます:
\begin{eqnarray}
\mathbb{E}[Y^{a=1}] &=& \beta_0 + \beta_1\\
\mathbb{E}[Y^{a=0}] &=& \beta_0\\
ATE &=& \beta_1
\end{eqnarray}
また、処理が連続のとき、以下のようなモデルが紹介されています:
\begin{eqnarray}
\mathbb{E}[Y^{a}] = \beta_0 + \beta_1 a + \beta_2 a^2
\end{eqnarray}
あくまでこれは2次式までを考慮した一例であり、実際にはより複雑なモデルを立てることもありえるということに注意してください。
パラメータ推定
MSM のパラメータ推定にあたって、 IPW によって重み付けした最小二乗法、通称 IP-WLS を用いる手法が 12.4 節で紹介されています。
実装は、Python の場合は statsmodels、R の場合は lm や gee を使うことになるでしょう。
パラメータの分散を推定する際には、厳密に解析するか、 bootstrap を使うか、サンドウィッチ分散を使うかの三択になるとも紹介されています。
また、P152 の左側には、 IP-WLS の結果が Hajek estimator と一致すると書かれています。
処置が2値の場合、本当に IP-WLS は Hajek estimator と一致するのか？
まず、一つ目の疑問に答えていきます。愚直に解析します。
個人 が処置
を受ける確率
] を
と表記すると、 IP-WLS は
\begin{eqnarray}
L = \sum_{i=1}^{n} \Biggl[
\frac{A_i}{\pi_i} \bigl(Y_i - \beta_0 - \beta_1 A_i \bigr)^2 + \frac{1-A_i}{1-\pi_i} \bigl(Y_i - \beta_0 - \beta_1 A_i \bigr)^2
\Biggr]
\end{eqnarray}
を最小化する問題を考えればよいことになります。偏微分を行った式
\begin{eqnarray}
\frac{\partial{L}}{\partial{\beta_1}} &=& 2\sum_{i=1}^{n} \Biggl[
\frac{A_i}{\pi_i}\bigl(Y_i - \beta_0 - \beta_1 \bigr)(-A_i) + \frac{1-A_i}{1-\pi_i} \bigl(Y_i - \beta_0 - \beta_1 A_i \bigr)(-A_i)
\Biggr] \\
&=& 2\sum_{i=1}^{n} \Biggl[
\frac{-A_i}{\pi_i}\bigl(Y_i - \beta_0 - \beta_1 \bigr)
\Biggr] \\
&=& 0
\end{eqnarray}
を整理すると、] の推定量は
\begin{eqnarray}
\sum_{i=1}^{n} \Biggl[
\frac{A_i}{\pi_i}\bigl(Y_i - \hat{\theta_1} \bigr)
\Biggr]
&=& 0
\end{eqnarray}
の解となります。
これを踏まえてさらに、
\begin{eqnarray}
\frac{\partial{L}}{\partial{\beta_0}} &=& 2\sum_{i=1}^{n} \Biggl[
\frac{-A_i}{\pi_i}\bigl(Y_i - \beta_0 - \beta_1 \bigr) - \frac{1-A_i}{1-\pi_i} \bigl(Y_i - \beta_0 - \beta_1 A_i \bigr)
\Biggr] \\
&=& -2\sum_{i=1}^{n} \Biggl[
\frac{1-A_i}{1-\pi_i} \bigl(Y_i - \beta_0 \bigr)
\Biggr] \\
&=& 0
\end{eqnarray}
を整理すると、] の推定量は
\begin{eqnarray}
\sum_{i=1}^{n} \Biggl[
\frac{1-A_i}{1-\pi_i} \bigl(Y_i - \hat{\theta_0} \bigr)
\Biggr]
&=& 0
\end{eqnarray}
の解になります。
これらの式を、前提知識の章のリンクで説明した Hajek estimator のモーメント法による定式化と比較すると、全く同じ形になっているということが確認できると思います。
したがって、 処置が2値のとき、 IPW で重み付けをした最小二乗法の結果は、確かに Hajek estimator と等しいことが示せました。
処置が多値のときはどうなるか？
what if book には処置が多値の場合については説明がされていないので、2値の場合をよしなに拡張して定式化を行います。
ある処置のレベル に対して、周辺構造モデルを以下のように表現します:
\begin{eqnarray}
\mathbb{E}[Y^{a=j}] = \beta_j
\end{eqnarray}
個人 が処置
を受ける確率
] を
と表記すると、 IP-WLS では
\begin{eqnarray}
L = \sum_{i=1}^{n} \sum_{j=1}^{J}
\frac{\delta(A_i-j)}{\pi_{ij}} \bigl(Y_i - \beta_j \bigr)^2 \tag{1}
\end{eqnarray}
を最小化する問題を考えればよいことになります。 はディラックのデルタ関数です。
\begin{eqnarray}
\frac{\partial{L}}{\partial{\beta_j}} &=&
-2\sum_{i=1}^{n} \frac{\delta(A_i-j)}{\pi_{ij}} \bigl(Y_i - \beta_j \bigr)\\
&=& 0
\end{eqnarray}
を整理すると、] の推定量は
\begin{eqnarray}
\sum_{i=1}^{n}
\frac{\delta(A_i-j)}{\pi_{ij}} \bigl(Y_i - \hat{\theta_j} \bigr)
&=& 0
\end{eqnarray}
の解になります。
多値の場合の Hajek estimator の定義は what if book には載っていなかったはずですが、この推定量は、2値の場合の Hajek estimator を素朴に拡張した式になっていることが確認できるかと思います。
M推定量の文脈による正当化（処置が離散の場合）
これまで、Hajek estimator との対応によって MSM の正当化を試みてきましたが、ここではM推定量の立場から改めて整理することを試みます。
以下の星野本の P81-82 を参考にします。
調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)
- 作者:星野 崇宏
- 発売日: 2009/07/29
- メディア: 単行本
まず、天下り式に、処置 に対する potential outcome とパラメータを引数にとった非負のスコア関数
というものを導入します。
二乗誤差の最小化を考える場合、以下のようなスコア関数を考えることになるでしょう:
\begin{eqnarray}
m_j(Y^{a=j}, \theta_j) &:=& -(Y^{a=j} - \theta_j)^2
\end{eqnarray}
さらに、以下のようなスコア関数の和の期待値を最大化したい、と考えたとします:
\begin{eqnarray}
\mathbb{E}_{\tilde{Y}} \Biggl[
\sum_{j=1}^{J} m_j(Y^{a=j}, \theta_j)
\Biggr] \tag{2}
\end{eqnarray}
ここでは、期待値は potential outcomes についてとっています。
この式からは、すべての処置の水準の重要度を等しく扱った上で、処置ごとの potential outcome をできる限り正しく推定したい という気持ちを感じることができますし、この気持ち自体をある意味で「自然」なものだとして正当化することは可能だと考えられます（私個人の感覚ですが）。
しかし残念なことに、式 (2) には counterfactual outcome が含まれているので、そのまま経験近似を行うことが不可能です。
そこで、式 (2) と期待値の意味で等しくて（不偏で）、かつ経験近似が容易に行える ような別の式を考えたくなります。
そのような性質を持つ式の一つが以下のような形のもの（期待値の中身）です。不偏性は conditional exchangeability の仮定によって示せます。
\begin{eqnarray}
\mathbb{E}_{\tilde{Y}, L, A} \Biggl[
\sum_{j=1}^{J} \frac{\delta(A-j)}{\pi_{j}} m_j(Y^{a=j}, \theta_j)
\Biggr] \tag{3}
\end{eqnarray}
そして、consistency の仮定を用いてこの式 (3) を経験近似したものが、式 (1) のIP-WLS であると解釈できます。
また、式 (3) をパラメータで微分してから、微分と積分が交換できることを仮定して経験近似をすると、M推定量を考えていることになるような気持ちになれます。
改めてまとめます。
- 「すべての処置の水準の重要度を等しく扱った上で、処置ごとの potential outcome をできる限り正しく推定したい」という気持ちを式 (2) として表現することを認めた上で
- 「式 (2) と期待値の意味で等しくて、かつ経験近似が容易に行える」ような便利な式を考えると
- 式 (3) の形は自然と導出され、推定の正しさを二乗誤差で測定することに同意すれば、その経験近似により IP-WLS の式が得られる（& M推定量として解釈できる）
というのがここでの主張になります。
一見突拍子もないように感じた IP-WLS が自然な導出により得られる、ということが共有できたかと思います。
M推定量の文脈による正当化（処置が連続の場合）
最後に、処置が連続の場合についても直感的な解釈を与えていきます。
ここから先の話はどの本にも載っていなかったので、自分の感覚を信じて論理を組み立てていきます。
まず、先ほどと同様に式 (2) のようなものを考えてみると、処置が連続の場合、処置について和ではなく積分を考える必要が出てくることがわかります。
また、すべての処置の水準の重要度を等しく扱おうとすると、処置の区間が有限でない場合積分値が無限に飛んでいってしまいます。
そこで、処置の密度関数 によって重み付けを行った上で、処置ごとの potential outcome をできる限り正しく推定したい という気持ちで式 (2) を修正してみます:
\begin{eqnarray}
\mathbb{E}_{\tilde{Y}} \Biggl[
\int_{a' \in \mathcal{A}} f(a') m(Y^{a=a'}, \theta, a') da'
\Biggr] \tag{4}
\end{eqnarray}
なお、ここから先は potential outcome を扱うときに を使った表記に切り替えます。
また、スコア関数 の引数に処置の情報を含むようにします。
式 (4) を見てみると、当然 potential outcomes は観測できないので、この最大化をそのまま考えるのは困難であり、代理の式を探したくなります。
処置が離散の場合を参考にして、 をかけて期待値をとってみると、
\begin{eqnarray}
\mathbb{E}_{\tilde{Y}, L, A} \Biggl[
\int_{a' \in \mathcal{A}} f(a') m(Y^{a=a'}, \theta, a') \frac{\delta(A - a')}{f(a' \mid L)} da'
\Biggr]
&=&
\int_{a' \in \mathcal{A}}
\mathbb{E}_{L}\Biggl[ \mathbb{E}_{A \mid L} \bigl[\frac{\delta(A - a')}{f(a' \mid L)} \bigr] \mathbb{E}_{Y^{a=a'}}[m(Y^{a=a'}, \theta, a')]
\Biggr] f(a')da' \\
&=&
\int_{a' \in \mathcal{A}}
\Biggl[\mathbb{E}_{Y^{a=a'}}[m(Y^{a=a'}, \theta, a')]
\Biggr] f(a')da'
\tag{5}
\end{eqnarray}
となり、式 (4) に対する不偏性を持つことが確認できます*2。
したがって、これを経験近似した以下の式 (6) を最大化するという操作には、処置が離散の場合と同様にM推定量の文脈からその正当性を与えられそうです。
\begin{eqnarray}
\sum_{i=1}^{n} \Biggl[
\int_{a' \in \mathcal{A}} \biggl( \frac{\delta(A_i - a') f(a')} {f(a' \mid L_i)} m(Y_{i}^{a=a'}, \theta, a') \biggr) da'
\Biggr]
&=&
\sum_{i=1}^{n} \Biggl[
\frac{f(A_i)} {f(A_i \mid L_i)} m(Y_{i}^{a=A_i}, \theta, A_i)
\Biggr]\\
&=&
\sum_{i=1}^{n} \Biggl[
\frac{f(A_i)} {f(A_i \mid L_i)} m(Y_{i}, \theta, A_i)
\Biggr]
\tag{6}
\end{eqnarray}
個人的には、不偏性を示すときと経験近似をするときとで、デルタ関数の処理が異なってくるというのがエモポイントです。
そして、式 (6) のスコア関数に二乗誤差を用いると stabilized weights を用いた IP-WLS そのものになります。
以上の議論により、処置が連続の場合の IP-WLS についても、M推定量の文脈での正当化を行うことができ、その意味で「自然な」推定手法だと解釈できると考えられます。
おわりに
本記事では、 IP-WLS で MSM のパラメータ推定を行うことの正当性について、Hajek estimator や M推定量との対応をとりながら紹介を行いました。
少し記述が回りくどくなってしまいましたが、モヤモヤを持たれている方の助けになれば幸いです。
誤りを見つけられた方は、そっと教えていただけると幸いです。
もし一般企業のデータ分析者がはなおでんがんの「最強の勝負めし分析」企画をやったら
これまでの記事では因果推論の真面目な話を書いてきましたが、今回は趣向を変えてポップなパロディ企画をやります。
記事の概要
ひとことで言うと、タイトルの通り、はなおでんがんさん（以下「はなでんさん」と略します）の動画 【全200試合】藤井七段の勝負メシの勝率から、最強の勝負メシを決めようではないか。 の検証を、データ分析者の立場からより厳密に行ってみようというものです。
はなでんさんのファンとしては、一度動画をご覧になっていただいた上で本記事を読んでいただけると嬉しいですが、動画の背景知識なしでも理解できるように書く予定です。
対象読者、読後イメージ
以下の3タイプの人を対象にします:
- 分析結果だけ知りたい人: 分析の全体まとめだけ読んでいただけると、そういう感じなのか〜という理解に至るかと思います。
- 分析の中身を知りたい人: PythonとRで可視化、検定、回帰する例を載せているので、もしよければ参考にしていただければと思います。
- 因果推論ガチ勢: IPWのところあたりを楽しんでいただければと思います。もし間違っていたら教えていただきたいです*1。
目次は以下になっています:
記事の構成
本記事では、分析結果を共有するときのフォーマットとして、YWTを拡張したものを使います。
まず、分析のフェーズに合わせていくつか大きな段落を作ります。
次に、それぞれの段落の中で、レポートと実装を分離します。レポートにしか興味のない人が余計なものまで見るコストを減らすためです。
最後に、レポートの中身を以下のように構造化します:
- B (Background): 背景を書きます。資料の最初の段落だけに書くことが多いです。
- P (Purpose): 段落の目的をシンプルに書きます。
- H (Hypothesis): 事前に持っている仮説をふわっと書いておきます。
- C (Conclusion): 結論や考察を書きます。次の段落やその後の意思決定に値する情報をシンプルに書きます。
- Y (やったこと): やったことを書きます。
- W (わかったこと): わかったことを事実ベースで書きます。
- T (次やること): 次にやること、やり残したことを書きます。Cと少し被るので厳密にはわけられないですが、Cよりは緩く書きます。
レポート部分は常体、レポート以外は敬体で記事を書く予定です。
分析の全体まとめ
分析結果をまとめます。忙しい人はここだけを見ていただければ大丈夫です。
B
- 冒頭に述べたはなでんさんの動画では、藤井聡太選手の年度ごとのデータを手動で集計し、勝率とご飯の関連を調べることで、「勝負めしとして何が適切か」を調べようとしていた
- 分析結果として「冷えたご飯はよくない」「カレーうどんと天丼がいい」という主張がされていた
- この分析は公開データの分析という点で興味深い試みであるが、以下3点で課題があると考えられる:
- 実際、はなでんさんの動画のコメント欄にも交絡について指摘をする人が存在していたことからも、因果についての分析を行うニーズはあるということが期待される
P
- 手動集計を自動化することにより再現性や拡張性を保証し、因果推論の手法を用いて交絡調整を行うことで因果関係についての主張を行う
- ただし、あくまでこれは動画企画のパロディ・ビッグバネイト・茶番であり、はなでんさんの動画を批判したり否定したりする意図は一切ないということに留意していただきたい
- また、本分析結果はあくまで現時点での一例であり、今後の追加分析によって主張がアップデートされる可能性があることにも留意していただきたい
H
- はなでんさんの分析結果には妥当性がありそうだが、何らかの交絡があるのではないか？
- 本当に検定結果が有意になるのか？
C
- 「冷たいご飯」や「カレーうどん」と勝率の間に一定の傾向はあるが、有意な関連ではなかった（「冷たいご飯だからダメ」と考えずに、冷たいものが食べたくなったら冷たいものを食べてもまあ統計的には大丈夫でしょう！）
- むしろ「うどん」や「そば」の方が関連が大きい
- 交絡調整をすると、「うどん or そば」or 「それ以外」の2水準に処置をわけたときの処置効果は有意ではなくなる（交絡調整しないときは有意になるので注意！）
- 交絡調整をしても、「うどん」「そば」「それ以外」の3水準に処置をわけたとき、「そば」を食べることの効果は有意にゼロより大きい（勝ちたいときはそばを食べてみよう！）
Y
W
- Cと同じ
T
- 藤井聡太さん以外のデータを集めてより一般性のある主張をする
- トレンドや場所などの情報を考慮してより正確な分析をする
基礎集計と分析設計
基礎集計と分析設計について詳しく説明します。
レポート
P
H
- はなでんさんの動画で参考にしていたページからスクレイピングすれば、食事名と勝敗のデータを簡単に取得できるのではないか
C
Y
- スクレイピング
- 対局一覧を https://shogi-sanpo.com/fujiisouta/result/ から取得し、各対局の詳細データをさらにスクレイピングして "fujii_shogi_meal.csv" として保存
- ご飯一覧を https://shogi-sanpo.com/fujiisouta/gourmet/ から取得し、"fujii_shogi_meal2.csv" として保存
- 不整合調査
- 2つのcsvと実際の対局記録から、データのズレをチェック
- 前処理
- 対局が2日にまたがった2件はリストワイズで除去（スクレイピングや集計が面倒）
- 店の名前はいったんは無視（分析目的からずれるのと、データに揺れがあるので）
- 1回目の食事名をfirst_mealとしてtreatmentにする（データ量の観点と、意味的にも妥当そう）
- 「不明」というデータが1つだけあったので欠損に置き換え
- 変数の分布理解
- 各変数の欠損パターンを把握
- outcomeとして、勝敗数の推移を把握
- treatmentとして、ご飯名の出現頻度を把握
W
-
- ご飯一覧のページは途中からデータの定義が変わっており、ある時期以前は詳細データのリンクまでたどることができないため、対局相手の情報を取得できない
- 対局一覧のページではすべての詳細データのリンクをたどることができるので、対局相手の情報はここから取得する必要がある
不整合調査
対局一覧がおかしいところが2点
- 20170810: 昼食の店の名前が間違っている（https://www.nikkansports.com/general/nikkan/news/1869967.html）
- 20181123: 夕食が昼食になっている（https://shogi-sanpo.com/fujiisouta/kisen/eiou/20181123/）
ご飯一覧がおかしいところが1点
- 20171102: 昼食の店の名前が間違っている（https://www.sankei.com/west/photos/171102/wst1711020048-p1.html）
どちらがおかしいか不明なところが1点
- 20180125: 夕食の味噌煮込みうどんがご飯一覧にのみ存在する
それ以外は店名ベースで見ると表記揺れ以外問題がなかった
変数の分布理解
- だいたいどの年も勝率は80%overをキープしている
- 2016, 2020年度は試合数が少ない
- 1回目の食事情報が含まれているのは148/218件で、67%ほど
- 食事名については対局一覧の方が表記揺れが多い
T
- 分析に入る
- 藤井聡太さん以外のデータを集める
- 「1回目の食事情報」よりもう少し深い情報（例えば夕食とおやつの考慮）を集める
- データをもう少し綺麗にする
実装
Jupyter notebook 上でスクレイピングと基礎集計を行いました。Python3.6です。
スクレイピングのコードやデータは公開できないです（スクレイピングの処理が一番大変でした）が、基礎集計部分は気が向いたらuploadします。
主要な処理のみ記事の中で紹介します。
importはこちらです:
%matplotlib inline import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns from IPython.display import display_html import researchpy
スクレイピングしてきた対局とご飯のデータはこのようになっています:
df = pd.read_csv("fujii_shogi_meal.csv")
df.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 218 entries, 0 to 217 Data columns (total 12 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 date 218 non-null object 1 title 218 non-null object 2 link 218 non-null object 3 description 218 non-null object 4 is_play_first 218 non-null bool 5 lunch_store 145 non-null object 6 lunch 146 non-null object 7 dinner_store 68 non-null object 8 dinner 70 non-null object 9 ct_win 215 non-null float64 10 ct_lose 215 non-null float64 11 win 218 non-null int64 dtypes: bool(1), float64(2), int64(1), object(8) memory usage: 19.1+ KB
218件なので多いとは言えないですが、一応集計が可能なレベルかとは思います。
変数の定義は以下です:
- date: 対局日付がyyyy/mm/ddで入っている - title: 対局名が入っている。竜王戦とか。 - link: 対局詳細のリンク。 - description: 対局の説明。 - is_play_first: 先行後攻のフラグ - lunch_store: 昼食をとった店の名前 - lunch: 昼食メニュー名 - dinner_store: 夕食をとった店の名前 - dinner: 夕食メニュー名 - ct_win: 相手の通算勝利数（対戦日まで） - ct_win: 相手の通算敗北数（対戦日まで） - win: 対局の勝敗（1が勝利、0が敗北）
データの不整合調査は泥臭い作業なので記事では省略します。
年度ごとの勝率の遷移はこのようになりました。めちゃくちゃ強いですね。年ごとのトレンドを考慮する必要性は（今のところ）それほどなさそうです。
df["date"] = pd.to_datetime(df["date"]) date_q = pd.PeriodIndex(df["date"], freq="Q") df["fiscal_year"] = date_q.map(lambda x: x.year - 1 if x.quarter == 1 else x.year) sns.pointplot(x="fiscal_year", y="win", data=df) plt.ylim((0, 1)) plt.title("勝率は80%以上をキープしている") plt.ylabel("勝率")
ちなみに、対局数は2016, 2020年が少ないので、解釈の際には注意してください:
df.groupby("fiscal_year")["win"].count().plot.bar() plt.title("2016, 2020年度は対局数が少ない") plt.ylabel("対局数")
対局一覧からご飯情報を集計してみると、以下のことがわかります:
- 食事情報が含まれているのは147/218回（うち1回だけ不明）で、67%ほど
- lunchなしdinnerありは1件しかない（ただしデータ不整合で確認したようにこの分類は必ずしも正確ではない）
- lunchがありのときにdinnerがあるかどうかは半分ずつくらいの割合
pd.crosstab(df.lunch.notnull(), df.dinner.notnull())
dinner False True lunch False 71 1 True 77 69
昼食夕食の揺れを排除するため、1回目の食事名に相当する変数を作ります:
df["first_meal"] = df["lunch"] df.loc[df["lunch"].isnull(), "first_meal"] = df["dinner"] df.loc[df.first_meal == "不明", "first_meal"] = np.nan
食事名の頻度を集計するとこのようになります:
plt.figure(figsize=(6, 10)) cnt = df.first_meal.value_counts() remove_cnt = sum(cnt == 1) cnt.loc[lambda x: x > 1][::-1].plot.barh() plt.xlabel("メニュー") plt.ylabel("注文回数") plt.title(f"1回目の食事の注文回数(1回しか注文されていない {remove_cnt} 種類のメニューは除外)")
しかし、実際に食事名で並び替えて一覧を見てみると、かなりの表記揺れ（大文字小文字、スペース有無 etc）が存在していることがわかりました。
そのため、食事名そのものではなく、表記揺れに気をつけつつざっと見て目立ったキーワードでデータを作り直す必要があると判断しました。
ご飯と勝率の分析
方針が立ったので、実際に関連を分析していきます。
やるだけなので、この段落はすごくシンプルです。
レポート
P
- キーワードをいくつか出して、勝率との関連を調べる
H
- 冷たいご飯は勝率にネガテイブな関連を示すのではないか
C
- 冷たいご飯ではなく、「うどん」や「そば」が有意な関連を示したが、因果的な解釈をできるかを追加で調べる必要がある
Y
- 冷たい食事フラグ、カレーうどんフラグを作って、勝率を検定
- 生データを見て頻繁に出てきたうどんとそばについての変数を作って、勝率を検定
W
- はなでん動画の仮説に反して、冷たいご飯やカレーうどんは、勝率との有意な関連はない
- 「うどん」と「そば」は勝率に対してポジティブな関連がないとは言えない
T
- キーワードの候補を増やす
- 交絡を調整しに行く
実装
先ほどと同様のJupyter notebook上で実装しました。
処置変数の候補を作ります:
df["cold_flag"] = df.first_meal.str.contains("冷") df["curry_udon_flag"] = (df.first_meal.str.contains("カレー")) & ((df.first_meal.str.contains("うどん")) ) df["hamburger_flag"] = df.first_meal.str.contains("ハンバーグ") df["udon_soba_else"] = df.first_meal.map( lambda x: x if x != x else "both" if "うどん" in x and "そば" in x else "udon" if "うどん" in x else "soba" if "そば" in x else "else") df["udon_or_soba"] = df.udon_soba_else.map(lambda x: x if x != x else x in ["udon", "soba"])
はなでんさんの動画で出ていた「冷たいご飯」の他に、目立ったキーワードをいくつか加えました。 カレーうどんとハンバーグは処置群が少なかったので分析しません。
さて、冷たいご飯について検定してみます:
crosstab, res = researchpy.crosstab(df.cold_flag, df.win, test= "chi-square", correction=True) print("分割表") display_html(crosstab) print("検定結果") display_html(res)
分割表 win win 0 1 All cold_flag False 16 103 119 True 6 21 27 All 22 124 146 検定結果 Chi-square test results 0 Pearson Chi-square ( 1.0) = 0.7276 1 p-value = 0.3937 2 Cramer's phi = 0.0706
ブログの都合上見にくくなっていますが、「冷たいご飯か否か」は勝率との関連は (5%) 有意でないという結果になりました。
分割表についての他の検定結果もすべて同様でした。
効果量も小さい（< 0.1）ので、この仮説は微妙そうだ、と言えそうです。
次に、「うどん」「そば」「その他」の3水準にわけた変数について調べてみます。
crosstab, res = researchpy.crosstab(df.udon_soba_else, df.win, test= "chi-square", correction=True) print("分割表") display_html(crosstab) print("検定結果") display_html(res)
分割表 win win 0 1 All udon_soba_else else 17 64 81 soba 0 22 22 udon 5 38 43 All 22 124 146 検定結果 Chi-square test results 0 Pearson Chi-square ( 2.0) = 6.5185 1 p-value = 0.0384 2 Cramer's V = 0.2113
この検定によって、udon_sobe_elseの水準は5%有意、つまり「関連がないとは言えない」ことがわかりました。
分割表についての他の検定結果もすべて同様でした。
効果量は中程度より少し弱め（0.21 ~ 0.25）ので、この仮説は比較的筋が良さそうだ、と言えそうです。
なお、「うどんかそば」と「それ以外」に水準をわけてみたところ、同様に「関連がないとは言えない」ことがわかりました。
次の段落ではこれらの処置についての検証を深ぼっていきます。
天気と相手の勝率による交絡調整
ようやく因果推論の話になります。天気と相手の勝率で交絡調整をしていきます。
レポート
B
- これまでの分析では、以下のような交絡が考慮されていない
- 「暑い日は冷たいものを注文しやすく、暑い日は負けやすいが、冷たいものを食べるかどうかと負けるかどうかには因果関係はない」という状況が真だったときに、「冷たいもの」と「勝敗」だけの関連を分析すると、「冷たいものを食べると負けやすい」といった誤った解釈に至る可能性がある
- このような、交絡を引き起こす「暑さ」という変数は交絡変数と呼ばれ、分析において調整を行う必要がある
P
- 交絡調整を行って分析を進め、因果的な解釈を行う。
H
- 天気、相手の勝率、体調、盤面の様子、気分 などが交絡変数になりそう（年度や場所の効果は2で微妙だったので行わない）
C
- 天気と相手の勝率の変数が交絡調整に使えると判断した
- 交絡調整をすると「うどん or そば」or 「それ以外」の処置効果は有意ではなくなる
- 交絡調整をしても「そば」を食べることの効果は有意にゼロより大きく、ポジティブと言えるであろう（勝ちたいときはそばを食べてみよう！）
Y
- 藤井聡太選手のインタビュー*4をもとに、食べるご飯をどのように決めているのかを調べて、交絡変数をリストアップした
- 重要そうな変数として「天気」と「相手の勝率」の2つを選択し、データを整形した
- 天気
- 多くの食事が昼間にとられるものなので、最高気温を使う
- 対局場所が簡単に見つからなかったので、東京のデータを気象庁から入手して代用した (http://www.data.jma.go.jp/gmd/risk/obsdl/index.php)
- 勝率
- 対戦相手の対戦日前までの通算勝率として表示されているデータから計算
- 1回しか戦績がないケースで勝率が100%になっている例は外れ値すぎるので、flat priorを使って補正（勝率の性質を考えると、真ん中らへんが下がっているJeffreys priorよりは妥当と判断）
- 天気
- 2つの変数でいくつかのtreatmentのmodelを作り、IPW によって交絡を調整した
W
- インタビュー記事を見ると、即決で食事を決めているとの発言がある
- 気温が高いと冷たいご飯を食べやすい
- 気温が低いとそばを頼みやすい
- 相手の勝率と冷たいご飯の関連はほとんどない
- 相手の勝率が高いときは「うどんやそば」以外を頼みやすい
- 気温の高さと藤井聡太さんの勝率には負の関連がある
- 相手の勝率と藤井聡太さんの勝率には負の関連がある
- 交絡調整の有無に関わらず、そばの処置効果だけが有意にゼロでなない
- 交絡調整をすると、「うどん or そば」の水準を一つにまとめた処置効果が有意でなくなる
- 交絡調整によってうどんやそばの回帰係数は小さくなった
T
- さらに交絡調整を行う。例えばご飯を食べる直前の盤面の有利不利のスコアなど
- 年度のトレンドをうまく反映して分析する
実装
前処理は先ほどと同じ Jupyter notebookで行い、回帰分析からは Rmarkdownで行いました。
Pythonでの処理
天気の変数は、気象庁から落としてきたデータから以下のように加工して結果を確認しました:
weather = pd.read_csv( "~/Downloads/temperature.csv", skiprows=[0,1,2,4,5], encoding='shift_jis') weather["date"] = pd.to_datetime(weather["年月日"]) weather["max_temperature"] = weather["最高気温(℃)"] plt.plot(weather.date, weather["max_temperature"])
:
特におかしな挙動はしていないですね。
相手の勝率は以下のように加工しました:
alpha = 1 beta = 1 df["ct_win_ratio"] = (df.ct_win + alpha) / (df.ct_win + df.ct_lose + alpha + beta)
joinして保存しました:
df_merge = df.merge(weather[["date", "max_temperature"]], on="date") df_merge[df_merge.cold_flag.notnull()].to_csv("~/Downloads/fujii_merge.csv", index=False) df_merge.to_csv("~/Downloads/fujii_merge_all.csv", index=False)
joinしたデータで相関係数を見ると、以下のことがわかります:
fig = plt.figure(figsize=(10, 7)) sns.heatmap( df_merge[["max_temperature", "ct_win_ratio", "win", "udon_or_soba", "cold_flag"]].astype(float).corr(), annot=True, fmt="1.2f" )
Rでの基礎集計
ここから先の分析は、Rを用いて行います。
あまりRに慣れていないので雰囲気で書いていきます。
まずは因果的な分析を行わないnaiveな集計と可視化を行います。
利用するライブラリを読み込みます:
library(ipw) library(tidyverse)
データを加工します:
df <- read.csv("Downloads/fujii_merge.csv") # 相手の勝率がない場合は0.5で埋める（1件しかない） df$ct_win_ratio[is.na(df$ct_win_ratio)] <- 0.5 # Rのipwでlogitモデルを使うときはtreatmentを0-1に変換しないとダメ df_cp <- df df_cp$cold_flag <- as.integer(df_cp$cold_flag) - 1
冷たいご飯のフラグについてnaiveな回帰をしてみると、「係数の推定値は負だが5%有意ではない」という先ほどと同様の傾向が得られました:
summary(lm(win ~ cold_flag, data=df_cp))
Residuals:
Min 1Q Median 3Q Max
-0.8656 0.1344 0.1344 0.1344 0.2222
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.86555 0.03287 26.332 <2e-16 ***
cold_flag -0.08777 0.07644 -1.148 0.253
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3586 on 144 degrees of freedom
Multiple R-squared: 0.009073, Adjusted R-squared: 0.002191
F-statistic: 1.318 on 1 and 144 DF, p-value: 0.2528
次に、「うどんとそばとその他」について、naiveに回帰をしてみると、「そばは有意に勝率を高めそう」という結果が得られました:
summary(lm(win ~ udon_soba_else, data=df_cp))
Residuals:
Min 1Q Median 3Q Max
-0.8837 0.0000 0.1163 0.2099 0.2099
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.79012 0.03926 20.127 <2e-16 ***
udon_soba_elsesoba 0.20988 0.08494 2.471 0.0147 *
udon_soba_elseudon 0.09360 0.06666 1.404 0.1625
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3533 on 143 degrees of freedom
Multiple R-squared: 0.04465, Adjusted R-squared: 0.03129
F-statistic: 3.341 on 2 and 143 DF, p-value: 0.03817
ただし、0 or 1のoutcomeを回帰した信頼区間が算出されているということに注意してください。
交絡を調べるために、covatiate と処置の関係性を可視化します。
まず、最高気温と冷たいご飯フラグの関係性を見てみると、気温が高いと冷たいご飯を頼みやすいことがわかります:
df_cp %>% mutate(cold_flag = as.factor(cold_flag)) %>% ggplot(aes(x=max_temperature, y = ..density..)) + geom_histogram(aes(fill=cold_flag), alpha=.2, position="identity", binwidth = 3) + geom_density(aes(colour=cold_flag), alpha=.2)
また、気温が低いとそばを頼みやすいこともわかります:
ggplot(df_cp, aes(x=max_temperature, y = ..density..)) + geom_histogram(aes(fill=udon_soba_else), alpha=.2, position="identity", binwidth = 3) + geom_density(aes(colour=udon_soba_else), alpha=.2)
さらに、相手の勝率が高いときは、「うどんやそば」以外を頼みやすい傾向が確認できます（考察: うどんやそばでは強敵に対峙するエネルギーが足りないのでしょうか？）:
ggplot(df_cp, aes(x=ct_win_ratio, y = ..density..)) +
geom_histogram(aes(fill=udon_soba_else), alpha=.2, position="identity", binwidth = .02) +
geom_density(aes(colour=udon_soba_else), alpha=.2)
次に、covariate と勝率の関係性について可視化します。
負けている試合の方が最高気温は高そうです:
df_all <- read.csv("Downloads/fujii_merge_all.csv") df_all %>% mutate(win = as.factor(win)) %>% ggplot(aes(x=max_temperature, y = ..density..)) + geom_histogram(aes(fill=win), alpha=.2, position="identity", binwidth = 3) + geom_density(aes(colour=win), alpha=.2)
また、負けている試合の方が相手の勝率は高そうです:
df_all %>% mutate(win = as.factor(win)) %>% ggplot(aes(x=ct_win_ratio, y = ..density..)) + geom_histogram(aes(fill=win), alpha=.2, position="identity", binwidth = .03) + geom_density(aes(colour=win), alpha=.2)
よって、最高気温と相手の勝率で交絡を調整する効果はありそうだということがわかります。
Rでの交絡調整
IPWを用いて交絡を調整します。Stabilized weightsを使います。
まずは冷たいご飯フラグを処置として処置のモデルを計算します:
model_ipw <- ipwpoint( exposure = cold_flag, family = "binomial", link = "logit", numerator = ~ 1, denominator = ~ max_temperature + ct_win_ratio, data = df_cp) df_cp$ipw_cold <- model_ipw$ipw.weights
weightsの分布です。いびつな分布にはなっていないのでよしとします:
ipwplot(weights = model_ipw$ipw.weights, logscale = FALSE, main = "Stabilized weights", xlim = c(0, 8))
IPWによって最高気温の分布が釣り合っていることはこちらで確認しました:
df_cp %>% mutate(cold_flag = as.factor(cold_flag), ipw = ipw_cold / sum(ipw_cold)) %>% ggplot(aes(x=max_temperature, y = ..density.., weight=ipw)) + geom_histogram(aes(fill=cold_flag), alpha=.2, position="identity", binwidth = 3) + geom_density(aes(colour=cold_flag), alpha=.2)
IPWで処置効果を推定した結果、やはり冷たいご飯フラグの係数は有意にはなりませんでした（95%信頼区間が0を含んでいます）:
set.seed(71) orig_boot <- function(N, df, treatment, weights){ ate <- numeric(N) for (i in 1:N){ ind <- sample(1:nrow(df), replace = TRUE) ate[i] <- ipw_hajek(df[ind,], treatment, weights[ind]) } c(mean(ate), sort(ate)[c(0.025*N, 0.975*N)]) } orig_boot(1500, df_cp, "cold_flag", model_ipw$ipw.weights)
# mean, 0.025%, 0.0975% [1] -0.06024249 -0.24196345 0.08885549
最後に、「うどんとそばとその他」の変数を処置として計算します。
model_ipw_udon_soba_else <- ipwpoint( exposure = udon_soba_else, family = "multinomial", link = "logit", numerator = ~ 1, denominator = ~ max_temperature + ct_win_ratio, data = df_cp) df_cp$ipw_udon_soba_else <- model_ipw_udon_soba_else$ipw.weights
先ほどと同じように結果を見ていきます。
weightの分布に大きな問題はなさそうです:
ipwplot(weights = model_ipw_udon_soba_else$ipw.weights, logscale = FALSE, main = "Stabilized weights", xlim = c(0, 8))
IPWによって最高気温の分布が釣り合っています:
df_cp %>% mutate(ipw = ipw_udon_soba_else / sum(ipw_udon_soba_else)) %>% ggplot(aes(x=max_temperature, y = ..density.., weight=ipw)) + geom_histogram(aes(fill=udon_soba_else), alpha=.2, position="identity", binwidth = 3) + geom_density(aes(colour=udon_soba_else), alpha=.2)
相手の勝率の分布も釣り合っています:
df_cp %>% mutate(ipw = ipw_udon_soba_else / sum(ipw_udon_soba_else)) %>% ggplot(aes(x=ct_win_ratio, y = ..density.., weight=ipw)) + geom_histogram(aes(fill=udon_soba_else), alpha=.2, position="identity", binwidth = .03) + geom_density(aes(colour=udon_soba_else), alpha=.2)
IPWで推定結果を見ると、やはりそばが強いです！有意！（うどんは有意でない）
orig_boot_3 <- function(N, df, weights){ ate1 <- numeric(N) ate2 <- numeric(N) for (i in 1:N){ ind <- sample(1:nrow(df), replace = TRUE) m <- lm(win~udon_soba_else, data=df_cp[ind,], weights = weights) ate1[i] <- m$coefficients[["udon_soba_elseudon"]] ate2[i] <- m$coefficients[["udon_soba_elsesoba"]] } c(mean(ate1), sort(ate1)[c(0.025*N, 0.975*N)], mean(ate2), sort(ate2)[c(0.025*N, 0.975*N)]) } orig_boot_3(1500, df_cp, model_ipw_udon_soba_else$ipw.weights)
# mean, 0.025%, 0.0975% (udon) | mean, 0.025%, 0.0975% (soba) [1] 0.09588222 -0.06569996 0.23156328 0.21019828 0.12049088 0.31626702
一方、udon_or_sobaという処置についてIPWで推定した結果、処置効果は有意ではないという結果になりました:
orig_boot(1500, df_cp, "udon_or_soba", model_ipw_udon_or_soba$ipw.weights)
# mean, 0.025%, 0.0975% [1] 0.05500092 -0.07112215 0.17096173
ついでに
うどんとそばとその他の変数が重要そうなので、もう少し調べてみます。
年度ごとの注文数を眺めてみると、1年目はうどんかそばを必ず食べていたという驚きの結果になりました。
また、今年度はまだ一度もそばを食べていません。
初めてそばを食べたときの結果が楽しみです。
df_cp %>% mutate(fiscal_year = as.factor(fiscal_year)) %>% ggplot(aes(fiscal_year)) + geom_bar(aes(fill=udon_soba_else))
勝率の遷移まで調べてみるとこのようになります。
序盤に「トレンドは考慮しない」と言いましたが、今年度はelseの勝率が高まってきているので、何かしら変化があったのかもしれません:
df_cp %>% mutate(fiscal_year = as.factor(fiscal_year)) %>% group_by(fiscal_year, udon_soba_else) %>% summarize(mean = mean(win_int), sd = sd(win_int)) %>% ggplot(aes(x=fiscal_year, y=mean, colour=udon_soba_else, group=udon_soba_else), alpha=.5) + geom_line() + geom_errorbar(aes(ymin = mean - sd, ymax = mean + sd, width = 0.3))
トレンド情報、対局場所の情報、盤面の情報などまだまだ考慮できていないものがあるので、本分析結果は暫定のものとして捉えていただけると幸いです。
分析に誤りがありましたら、そっと教えていただけると幸いです。
謝辞
以下の方々に感謝します。皆さんの益々のご活躍をお祈り申し上げます。
おわりに
そばを食べたくなってきました。
*1:モデルの評価や残差分析は今後の課題とします
*2:興味のある処置とoutcomeの共通の原因によって発生するバイアス
*3:情報解析目的であること、特別な規約が書かれていなかったことから、負荷をかけすぎないアドホックな処理であれば問題ないと判断しました
*4:https://www.chunichi.co.jp/amp/article/92847
*5:こちらを参考にしました: https://qiita.com/saltcooky/items/451b96b3f346cb93a0b4
IPW 推定量の漸近分散についての補足
過去の記事の中で、 IPW の漸近分散について、以下の主張を行っていました。
よって、 Potential outcome の符号が等しければ右辺が0以上になり、「Horvitz-Thompson estimator より Hajek estimator の方が漸近分散が小さい」という主張が成立すると考えられます。
しかし、 @BluesNoNo さんとやりとりをしていく中で、 の値に着目することで別の条件を考えられる可能性を教えていただきました。
ありがとうございます．自信は全くありませんが，単純計算で，
— Tarotan (@BluesNoNo) June 2, 2020
w1=E[1/π], w2 = E[1/(1-π)]としたら，
(13)式 = w1 θ1^2 + w0 θ0^2 - (θ1 - θ0)^2
= (w1 - 1) θ1^2 - 2 θ0 θ1 + (w2 - 1) θ2^2
となり，これが0以上になるのは，1 < (w1 - 1)(w2 - 1)
となる気もします．間違えていたら，すみません．
その後、さらに式展開を行っていく中で、特別な条件なしで漸近分散の比較ができそうだということがわかってきたので、本記事の中で補足を行いたいと思います。
記事のゴール
本記事では、以下の主張を行うことをゴールにします:
- Horvitz-Thompson estimator より Hajek estimator の方が漸近分散が大きくなることはない（傾向スコアモデルgivenのとき）
新規性
以下の2点で新規性があると考えています。
- 上記の主張を（少なくとも日本語で簡単に）示したこと
- その過程で共分散についての簡単な補題を示したこと
補題については車輪の再発明も含んでいそうですが、証明を探すのに苦労した（結局自分で示しました）ので、日本語で必要な情報をサクッとまとめているという点で、一応新規性としておきます*1。
これ以降は証明をするだけなので、証明に興味がある方のみご覧いただければと思います。
過去の記事のおさらい
過去の記事では、傾向スコアモデルが与えられたもとで、以下のような式展開により、 「Potential outcome の符号が等しければ、 Horvitz-Thompson estimator より Hajek estimator の方が漸近分散が小さい」という主張に至っていました。
\begin{eqnarray}
Var_{HT}(\hat{\theta}_{1} - \hat{\theta}_{0}) - Var_{Hajek}(\hat{\theta}_{1} - \hat{\theta}_{0})
&=& \mathbb{E}\Bigl[ \frac{\theta_1^{2}}{\pi} \Bigr]
+ \mathbb{E}\Bigl[ \frac{\theta_0^{2}}{1-\pi} \Bigr]
- (\theta_1 - \theta_0)^2 \\
&>& \theta_1^2 + \theta_0^2 - (\theta_1 - \theta_0)^2 \ \ \ (\because 0 < \pi < 1) \\
&=& 2\theta_1\theta_0
\tag{1}
\end{eqnarray}
新たな主張
記事の主張を定理にすると、以下になります:
[Theorem 1]
\begin{eqnarray}
Var_{HT}(\hat{\theta}_{1} - \hat{\theta}_{0}) - Var_{Hajek}(\hat{\theta}_{1} - \hat{\theta}_{0})
&\ge& 0
\tag{2}
\end{eqnarray}
以下の流れで証明を行っていきます:
- 式1の中でいきなり不等式を作るのではなく、
を使ったまま式を展開する
- 二次式が出てくるので最小値を調べてみる
- 共分散の符号を調べる補題に落とし込む
二次式を作るところまで
まず、改めて式1を展開をしていきます。
\begin{eqnarray}
w_1 :&=& \mathbb{E}\bigl[\frac{1}{\pi}\bigr] \\
w_0: &=& \mathbb{E}\bigl[\frac{1}{1-\pi}\bigr] \\
\mathbb{E}\Bigl[ \frac{\theta_1^{2}}{\pi} \Bigr]
+ \mathbb{E}\Bigl[ \frac{\theta_0^{2}}{1-\pi} \Bigr]
- (\theta_1 - \theta_0)^2
&=& \bigl(w_1- 1\bigr) \theta_1^2
+ \bigl(w_0 - 1\bigr) \theta_0^2
+ 2\theta_1\theta_0
\tag{3}
\end{eqnarray}
ここで、 なので、両辺を
で割っても符号は変わりません。実際に割ってみると、
\begin{eqnarray}
\biggl(\theta_1 + \frac{\theta_0}{w_1-1}\biggr)^2
+ \frac{w_0 - 1}{w_1 - 1}\theta_0^2 - \frac{1}{(w_1-1)^2}\theta_0^2
&\ge& \frac{\theta_0^2}{(w_1-1)^2}\bigl( (w_1-1)(w_0-1)-1\bigr)
\tag{4}
\end{eqnarray}
のように計算でき、Theorem 1 が成立するには以下の条件が成立すればよいことがわかります:
\begin{eqnarray}
\bigl(w_1-1)(w_0-1) \ge 1
\tag{5}
\end{eqnarray}
共分散の符号を調べる補題への落とし込み
式5に をかけた上で再度
を使って書いてみると、以下のように計算できます:
\begin{eqnarray}
-\mathbb{E}\bigl[\frac{1}{\pi}\bigr] \mathbb{E}\bigl[\frac{1}{1-\pi}\bigr]
+ \biggl(\mathbb{E}\bigl[\frac{1}{\pi}\bigr] + \mathbb{E}\bigl[\frac{1}{1-\pi}\bigr] \biggr)
&=& -\mathbb{E}\bigl[\frac{1}{\pi}\bigr] \mathbb{E}\bigl[\frac{1}{1-\pi}\bigr]
+ \mathbb{E}\bigl[\frac{1}{\pi}\frac{1}{1-\pi}\bigr]\\
&\le& 0
\tag{6}
\end{eqnarray}
ここで、 はランダムな共変量によって決まる確率変数であるので、式6は
と
の共分散がゼロ以下であるという意味になります。
よって、共分散についての補題2を示すことにより、Theorem 1 が示せます*2。
補題 1
Lemma 1
\begin{eqnarray}
\text{Let} \ C \ \text{be a covariance of two random variables} \\
\text{and} \ X \ \text{be a random variable s.t.} \ 0 < X.\ \text{Then,}\\
C\biggl(X, \frac{1}{X}\biggr) &\le& 0
\tag{7}
\end{eqnarray}
Proof of Lemma 1
\begin{eqnarray}
C\biggl(X, \frac{1}{X} \biggr)
&=& \mathbb{E}\bigl[X \cdot \frac{1}{X}\bigr] - \mathbb{E}[X]\mathbb{E}\bigl[\frac{1}{X}\bigr] \\
&=& 1 - \mathbb{E}[X]\mathbb{E}\bigl[\frac{1}{X}\bigr] \\
&\le& 0 \ \ \ (\because \text{Jensen's inequality and} \ X > 0)
\tag{8}
\end{eqnarray}
補題 2
Lemma 2
\begin{eqnarray}
\text{Let} \ C \ \text{be a covariance of two random variables} \\
\text{and} \ X \ \text{be a random variable s.t.} \ 0 < X < 1.\ \text{Then,}\\
C\biggl(\frac{1}{X}, \frac{1}{1-X}\biggr) &\le& 0
\tag{7}
\end{eqnarray}
Proof of Lemma 2
\begin{eqnarray}
t_1 &:=& \frac{1}{X}\\
t_0 &:=& \frac{1}{1-X}
\tag{8}
\end{eqnarray}
とおくと、以下の関係式を得られます:
\begin{eqnarray}
t_1 &>& 1\\
t_0 &>& 1\\
\frac{1}{t_1} &=& 1 - \frac{1}{t_0}\\
t_0 &=& \frac{t_1}{t_1 - 1}\\
&=& 1 + \frac{1}{t_1 - 1}
\tag{9}
\end{eqnarray}
これらを用いると、期待値の線形性や共分散の性質から、
\begin{eqnarray}
C\biggl(\frac{1}{X}, \frac{1}{1-X}\biggr)
&=& \mathbb{E}\biggl[\frac{1}{X} \cdot \frac{1}{1-X}\biggr]
- \mathbb{E}\biggl[\frac{1}{X}\biggr]\mathbb{E}\biggl[\frac{1}{1-X}\biggr] \\
&=& \mathbb{E}\biggl[ t_1 \cdot \biggl(1 + \frac{1}{t_1 - 1}\biggr)\biggr]
- \mathbb{E}\biggl[ t_1 \biggr] \mathbb{E}\biggl[1 + \frac{1}{t_1 - 1}\biggr] \\
&=& \mathbb{E}\biggl[\frac{t_1}{t_1 - 1}\biggr]
- \mathbb{E}\biggl[ t_1 \biggr] \mathbb{E}\biggl[\frac{1}{t_1 - 1}\biggr] \\
&=& C\biggl(t_1, \frac{1}{t_1 - 1}\biggr) \\
&=& C\biggl(t_1-1, \frac{1}{t_1 - 1}\biggr) \\
&\le& 0 \ \ \ (\because \text{Lemma 1})
\tag{10}
\end{eqnarray}
となるので、題意が示されました*3。
まとめ
以上のように、推定量の漸近分散の比較を詳しく行い、傾向スコアモデルgivenのときには「Horvitz-Thompson estimator より Hajek estimator の方が漸近分散が大きくなることはない」ことを示しました。
共分散の符号の補題については、よく使いそうなものであるにも関わらずピンポイントな主張をすぐに見つけられず、自分で示した方が早いだろうと判断して証明してみました。
証明の誤りを見つけられた方、あるいは補題の証明について言及されているよりよい資料を見つけられた方がいらっしゃいましたら、そっとご指摘いただけると幸いです。
このような記事を書くきっかけを作ってくださった @BluesNoNo さん、ありがとうございます。
因果推論における standardization と parametric g-formula の関係性
過去の記事では、因果推論の中で重要な手法の一つである IPW の概要や疑問点について整理してきました。
今回は、 IPW と双璧をなす重要な手法である Standardization（標準化） について簡単に紹介します。
これまで同様、what if book を中心に議論していきます。
目次はこちらです。以前の記事よりはボリュームを抑えています。
- 記事のゴール
- 新規性
- what if book 2章で紹介された標準化のおさらい
- what if book 2章の標準化と13章の parametric g-formula の対応
- おまけ: conditional effect と標準化
- まとめ
what if book の主張を紹介した後で、数式部分を少しだけ補足します。
記事のゴール
本記事では、single time point exposure の条件下での平均因果効果の推定にあたって、以下の主張を行うことをゴールにします:
- what if book 2章の標準化と13章の parametric g-formula は、 outcome model について共変量で期待値をとっているという意味で統一的に見ることができるが、共変量の分布の扱い方によっては推定結果に違いが生じうる
Notation や仮定は冒頭に紹介した過去の記事と同じものを使います。
新規性
記事の主張について明確に述べている資料は見つからなかったので、一応それを新規性とします（ほんの少し式を補足しただけですが）。
what if book 2章で紹介された標準化のおさらい
標準化は、 what if book では2章と13章で登場します。
ここでは、2章の主張をおさらいします。
2章では、共変量が離散の場合に、以下のように potential outcome を推定できることが紹介されています:
\begin{eqnarray}
\mathbb{E}[Y^{(a)}]
&=& \sum_{l} \mathbb{E}[Y^{(a)} \mid L=l] \ \Pr[L=l] \ \ \ (\because \text{definition of marginalization}) \\
&=& \sum_{l} \mathbb{E}[Y^{(a)} \mid L=l, A=a] \ \Pr[L=l] \ \ \ (\because \text{conditional exchangeability}) \\
&=& \sum_{l} \mathbb{E}[Y \mid L=l, A=a] \ \Pr[L=l] \ \ \ (\because \text{consistency})
\tag{1}
\end{eqnarray}
最後の行の summation の中にある期待値と確率分布をそれぞれ観測データから推定すればよいということになり、以下の式で最終的な potential outcome の推定を行います:
\begin{eqnarray}
\sum_{l} \hat{\mathbb{E}}[Y \mid L=l, A=a] \ \hat{\Pr}[L=l]
\tag{2}
\end{eqnarray}
what if book 2章の標準化と13章の parametric g-formula の対応
次に、what if book 2章と13章の対応を考え、それらを統一的に見た上で、違いが生じうる部分について簡単に考察します。
13章のおさらい
13章では以下の2段階で議論が展開されています:
- 標準化は、outcome model について共変量で期待値をとる手法として考えられる
- outcome regression の予測結果について sample mean をとることでその期待値をいい感じに推定できる
打ち切り変数 については無視した上で、議論を追っていきます。
共変量で期待値をとっているという部分は以下の式で書けます:
\begin{eqnarray}
\mathbb{E}[Y^{(a)}]
&=& \mathbb{E}_{l} [\mathbb{E}[Y^{(a)} \mid L=l]] \ \ \ (\because \text{definition of marginalization}) \\
&=& \mathbb{E}_{l} [\mathbb{E}[Y^{(a)} \mid L=l, A=a]] \ \ \ (\because \text{conditional exchangeability}) \\
&=& \mathbb{E}_{l} [\mathbb{E}[Y \mid L=l, A=a]] \ \ \ (\because \text{consistency})
\tag{3}
\end{eqnarray}
によって共変量で期待値をとっていることを表現しました。
2章の標準化では共変量が離散の場合の表現しか与えられていませんでしたが、期待値の形で書くことで、共変量が連続の場合も表現できるようになりました。
その上で、 の期待値については outcome regression によって推定を行い、共変量で期待値をとる部分については観測データによる経験近似を行う以下の式が紹介されています:
\begin{eqnarray}
\frac{1}{n} \sum_{i=1}^{n} \hat{\mathbb{E}}[Y \mid L=L_i, A=a]
\tag{4}
\end{eqnarray}
これが parametric g-formula です。
outcome のモデルが特定されていて、かつ観測データが i.i.d. で得られていることを仮定すれば、求めたい期待値をいい感じに推定できそうです。
共変量については観測データ の値を使い、処置については興味のある処置
の値を固定している（処置については観測データではない）というところが肝になります。
2章との対応
what if book を読まれた方の中には、2章の標準化と13.3節の parametric g-formula の数式（式2と式4）間の対応がピンと来ていない方がいるかもしれないので、簡単に説明します。
結論としては、共変量の分布をどのように扱うかによって、同値になったりならなかったりする という話になります。
共変量が離散の場合、共変量の分布は以下のように推定されることが多いでしょう（ただの集計です）:
\begin{eqnarray}
n_l &:=& \sum_{i=1}^{n} I(L_i, l) \\
\hat{\Pr}[L=l] &=& \frac{n_l}{n}
\tag{5}
\end{eqnarray}
このとき、式2は以下のように展開できます:
\begin{eqnarray}
\sum_{l} \hat{\mathbb{E}}[Y \mid L=l, A=a] \ \hat{\Pr}[L=l]
&=& \sum_{l} \hat{\mathbb{E}}[Y \mid L=l, A=a] \ \frac{n_l}{n}\\
&=& \sum_{l} \frac{\sum_{i=1}^n I(L_i, l)\hat{\mathbb{E}}[Y \mid L=L_i, A=a]}{n_l} \ \frac{n_l}{n}\\
&=& \sum_{l} \frac{\sum_{i=1}^n I(L_i, l)\hat{\mathbb{E}}[Y \mid L=L_i, A=a]}{n}\\
&=& \frac{1}{n} \sum_l \sum_{i=1}^n I(L_i, l)\hat{\mathbb{E}}[Y \mid L=L_i, A=a] \\
&=& \frac{1}{n} \sum_{i=1}^n \hat{\mathbb{E}}[Y \mid L=L_i, A=a]
\tag{6}
\end{eqnarray}
最後の行は式4と全く同じ形になるので、式5のように共変量の分布を推定した場合、2章の標準化と13章の parametric g-formula は同じものとして対応がとれることがわかります。
逆に、2章の標準化にあたって共変量の分布の推定方法を変えた場合（例: 適当な prior を置いてベイズ推定する）、parametric g-formula による推定結果とは異なる結果が得られうることがわかります。
同様に、共変量が連続であるときに、「共変量の分布を推定した上でその分布を明示的に使って期待値をとるという手法」と 「parametric g-formula のように共変量の分布を推定しない手法」を比較すると、やはり推定結果が異なりうると言えるでしょう。
おまけ: conditional effect と標準化
標準化は marginal effect を推定するための手法であるため、基本的には conditional effect の推定には使えません*1。
一般に、 conditional effect を推定する際には、outcome regression や Marginal Structural Model や g-estimation を利用することになると思われます。
まとめ
what if book の2章と13章の数式を繋ぐことを目的に記事を書いてみましたが、意外と非自明なことが少なく、かなり内容の薄い記事になってしまいました。
もし同じような引っかかりを感じた方の理解の助けになれば幸いです。
*1:marginal effect を推定するために、 conditional effect を推定する手法の一つである outcome regression に修正を加えたものが標準化という認識です
色々なIPWの整理 〜 Stabilized weights の使い所 〜 (2)
前回の記事に引き続き、 IPW についての連載第2弾です。
今回も what if book を中心に議論していきます。
目次はこちらです。
- 記事のゴール
- 新規性
- 前提知識
- IPWの目的
- what if book 12.3 節の紹介
- what if book 12.3 節の補足と修正提案
- Doubly robust 推定量と 様々な IPW 推定量
- まとめ
IPW や Stabilized weights についての what if book の主張を紹介した後で、Stabilized weights の使い所についていくつかの角度から説明していきます。
記事のゴール
前回の記事では、single time point exposure の条件下での平均因果効果の推定にあたって、以下の2つの主張について説明しました:
- IPW によって処置
の Potential outcome
] を推定するときの基本は、
] を estimand とした Horvitz-Thompson estimator の推定である
- Hajek (modified Horvitz-Thompson) estimator は不偏推定量ではないが、いくつかの仮定のもとで Horvitz-Thompson estimator よりも漸近分散が小さい
本記事では、前回の記事で4つ目の主張として紹介していた以下の内容について説明することをゴールにします:
- Stabilized weights は Hajek estimator を推定するときに有用かもしれないが、他の推定量を推定するときには注意が必要 (特に、Doubly robust では適切な使用方法がわからない)
Notationは前回の記事を踏襲します。
新規性
新規性が気になる方のために、既存の資料と比較しておきます。
以下の点で新規性があると考えています:
- IPW において、 stabilized weights を使うことが妥当と思われる条件を調べ、 stabilized weights の安易な利用に警鐘をならした
- what if book における IPW と exchangeability と stabilized weights の関係性の不明点を列挙した（列挙しただけ）
- Doubly robust 推定量において stabilized weights を使うべきではないということを理論的な背景から説明した
前提知識
前回の記事 (1) の Notation と、 Horvitz-Thompson estimator と Hajek estimator の定義を理解していることを前提知識にします。
IPWの目的
Stabilized weights を理解するには、「逆確率で重みづけすることの意味や目的」について整理する必要があると考えているので、その部分の説明から始めます。
what if book の2章の紹介
前回の記事でも軽く触れたのですが、 IPW の目的は「データを augmentation することによって、exchangeability が成立するような擬似データセットを作ること」と言えます。
この件について、以前勉強会で私が発表を行ったときに、「IPW はピコ太郎だ」という旨のスライドを作成しました:
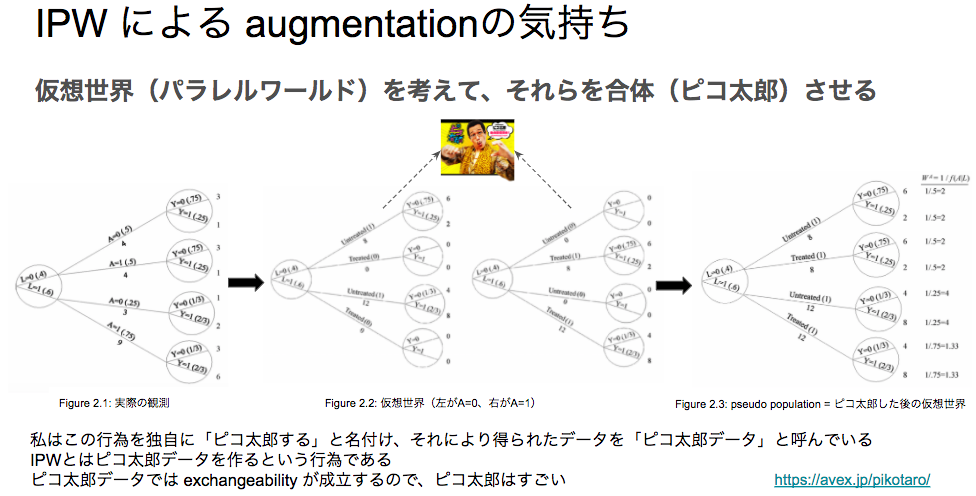
スライドに掲載している図はすべて what if book の2章から拾ってきている*1のですが、「介入が行われた世界線と、行われなかった世界線を考えて、それらを（ピコ太郎のように）合体させた pseudo population（擬似データセット） を作ること」を IPW の目的だと主張するものです。
逆確率を用いてサンプルを重みづけすれば、そのような擬似データセットを作成することができます。
擬似データセットの特徴としては、 what if book の Figure 2.3 の手前で以下のように述べられています:
Under conditional exchangeability in the original population, the treated and the untreated are (unconditionally) exchangeable in the pseudo-population because the L is independent of A
つまり、共変量と処置が独立になり、（条件づきではない）exchangeability が成立するということです。
そして、以下の文が続きます:
That is, the associational risk ratio in the pseudo-population is equal to the causal risk ratio in both the pseudo-population and the original population
exchangeability が成立することで、擬似データにおける関連のリスク比と、擬似データにおける因果のリスク比と、元のデータにおける因果のリスク比がすべて一致すると述べられています。
なお、処置が二値の場合、因果のリスク比は以下のように定義されます:
\begin{eqnarray}
\frac{\mathbb{E}[Y^{a=1}] }{ \mathbb{E}[Y^{a=0}] } \tag{1}
\end{eqnarray}
さらに、 Technical Point 2.3 では、逆確率を用いて擬似データセットを作ることで、リスク比が一致するだけでなく、 Potential outcome の期待値についての以下の等式も成立することが示されています:
\begin{eqnarray}
\mathbb{E}[Y^{(a')}] = \mathbb{E} \Bigl[ \frac{I(A, a')Y}{f_{A \mid L}(a' \mid L)} \Bigr] \tag{2}
\end{eqnarray}
この等式が成立することから、因果のリスク比が関連のリスク比と一致することも自明ですし、因果のリスク差（ATE）が関連のリスク差と一致することも自明なので、 IPW の有用性を感じられるかと思います。
2章の主張への疑問点
先ほど「exchangeability が成立する」と述べましたが、 what if book の中で厳密な証明を発見することができませんでした*2。
ただし、これまでの流れから察するに、共変量と処置の独立性からpseudo-population の世界において確率変数の意味での exchangeability が成立するということは言えるかもしれません。
また、式 (2) によって 「pseudo-populationでの期待値と元のデータのpotential outcomeの期待値が一致する」 という（2つのデータ間のmean exchangeability のような）ことは言えたと思います。
しかし、pseudo-population の世界において確率変数の意味での exchangeability が成立することが何に使えるのか ということは明記されておらず、なぜこのようなことを考えたいのかが不明瞭であるように感じました（Technical Point 2.3が pseudo-population の世界における確率変数の意味での exchangeability とどう結びつくのがわからないです）。
今後この記事の中で何度か exchangeability についての言及を行いますが、このあたりが曖昧なままになっているということを前提にお読みいただけると幸いです。
what if book 12.3 節の紹介
Stabilized weights について最も丁寧に述べている資料は what if book 12.3 節だと思うので、そこで述べられている内容を紹介します。
12.3 節の主張をまとめると「IPW の目的を踏まえると、必ずしも逆確率で重みづけを行わなくてもよい」というものになります。
色々な擬似データセットの生成
12.3節の冒頭では、 IPW の目的が共変量と処置の関連がないような（exchangeabilityが成立するような）擬似データセットの作成だということが再度強調されています。
The goal of IP weighting is to create a pseudo-population in which there is no association between the covariates L and treatment A
そして、逆確率による重みづけは、 そのような特徴を持つデータセットのクラスの中で、元のデータの2倍の大きさの擬似データセットを作成していることになると説明されています:
\begin{eqnarray}
\mathbb{E}_{A}\Bigl[\frac{1} { f_{A \mid L}(A \mid L=l) } \Bigr] = \frac{\Pr[A=1 \mid L=l] }{ f_{A \mid L}(1 \mid L=l)} + \frac{ \Pr[A=0 \mid L=l] }{ f_{A \mid L}(0 \mid L=l)} = 2 \tag{3}
\end{eqnarray}
しかし、ここで「共変量と処置が独立になるような擬似データセットを作る方法は他にもある」という主張がされています:
However, there are other ways to create a pseudo-population in which L and A are independent.
その直後に直感的な説明として、「逆確率に一律 をかけたもので重みづけをしても、 exchangeability への影響はなくて、かつ擬似データセットのサイズは元のデータと同じになる」という主張がされています。
詳しくは、擬似データセットについての定理により正当化されています。
擬似データセットについての定理
Technical Point 12.2 では、任意の関数 （正の値をとる必要がある）を使って重みづけを行うことに妥当性があるということを、Estimand が Potential outcome の期待値と等しくなる式によって説明しています。
すなわち、以下が成立することをもって、どんな関数を使っても妥当だという話になっています。
\begin{eqnarray}
\frac{\mathbb{E} \Bigl[ \frac{I(A, a')Y}{f_{A \mid L}(a' \mid L)} g(A) \Bigr]}
{\mathbb{E} \Bigl[ \frac{I(A, a')}{f_{A \mid L}(a' \mid L)} g(A) \Bigr]}
&=&
\frac{\mathbb{E}[Y^{(a')}] g(a')} {g(a')} \\
&=& \mathbb{E}[Y^{(a')}]
\tag{4}
\end{eqnarray}
どの関数を使うべきか
関数 として、処置の確率
ないしはその推定結果を使うべきだという主張がされています。
このとき、実際の推定は以下のように行われます:
\begin{eqnarray}
\frac{\sum_{i=1}^{n} \Bigl[ \frac{\hat{f}(A_i)}{\hat{f}_{A \mid L}(A_i \mid L_i)}I(A_i, a')Y_i \Bigr]}
{\sum_{i=1}^{n} \Bigl[ \frac{\hat{f}(A_i)}{\hat{f}_{A \mid L}(A_i \mid L_i)} I(A_i, a')\Bigr]}
\tag{5}
\end{eqnarray}
ここで使われた重みのことを stabilized weights と定義しています。
Stabilized weights を使うべき理由として、 Estimand が変わらないという条件を満たしつつ、一定の条件のもとで信頼区間が小さくなることを挙げられています。
また、effect modifier が存在するときは、effect modifier で条件づけた処置確率の推定結果を使うことが良しとされています。
what if book 12.3 節の補足と修正提案
以上をご覧になった方は、stabilized weights は素晴らしいもので、 IPW を考えるときにはなんでもかんでも stabilized weights を使えばいいような気持ちになるかもしれません。
しかし、ここから先では、 stabilized weights をそのまま使うと誤った解釈に至りうるケースについての指摘を行おうと思います。
ここでの結論は以下のようになります:
- Technical Point 12.2 は Hajek estimator を Estimand にした場合の話であり、それ以外の推定量について同様の等式が成り立つという保証はないのでは？
- 例えば、 Horvitz-Thompson estimator を Estimand にしたときは補正が必要になる（というかそもそも Horvitz-Thompson estimator で stabilized weights を使っても意味がない）のでは？
擬似データセットについての定理の補足
Technical Point 12.2 では、 Estimand が Potential outcome の期待値と等しくなる式を紹介しています。
しかし、前回の記事を読んでいただいた方はわかると思うのですが、これは Hajek estimator を Estimand とした場合の式展開になります。
Horvitz-Thompson estimator を Estimand にしたときは以下のように計算できます:
\begin{eqnarray}
\mathbb{E} \Bigl[ \frac{I(A, a')Y}{f_{A \mid L}(a' \mid L)} g(A) \Bigr]
&=&
\mathbb{E}[Y^{(a')}] g(a') \\
\tag{6}
\end{eqnarray}
つまり、stabilized weights を使った場合、 の逆数をかける必要が出てきます。
ただし、式を見るとわかるように、計算結果全体に対して を一律でかけただけになっているので、そもそもこの場合は stabilized weights を使う意味がありません。
このように、なんでもかんでも stabilized weights を使うべきとは言えない上に、誤った使い方をすると推定結果がおかしな値になってしまう可能性があります。
Technical Point 12.2 ではこうした前提条件が明示的に記述されていなかったため、誤った使い方をしてしまうリスクが一定存在すると考えられ、本記事で補足を行う価値があると判断しました*3。
Technical Point 12.2 以外の記述について
Stabilized weights を使うことの妥当性が Technical Point 12.2 に依存しているのであれば、 12.3 節の中で直感的な説明を行う部分についても、Technical Point 12.2 の前提条件（Hajek estimator の推定であること）を明示した方がよいと考えています*4。
逆にいうと、「他の推定量を扱う場合に、stabilized weights を使うことの妥当性がどのような直感で説明されるのか」という説明があるとより親切だと感じました*5。
また、 Hajek estimator を紹介するときに、 「重みづけするweight のスケーリングに対して、少なくとも Estimand の世界では計算結果が不変*6」といった特徴を記載してもよいのではないかと感じました。
Doubly robust 推定量と 様々な IPW 推定量
IPW を使った手法として、Doubly robust という便利なものが知られています。
記事の締めくくりとして、 Doubly robust 推定量 と 様々な IPW 推定量の関係性についての私見を述べます。
結論としては、以下になります:
- Horvitz-Thompson estimator 以外の IPW 推定量を Doubly robust で使うのは難しい（方法がわからない）
- 例えば、 Stabilized weights をむやみに Doubly robust で使うのは危険
Doubly robust 推定量
IPW では、傾向スコアモデルが正しく推定されていた場合、因果効果の推定結果にバイアスがのらないという保証はできません。
また、アウトカム回帰モデルを利用した Standardization*7 では、回帰モデルが誤って推定されていた場合、因果効果の推定結果にバイアスがのらないという保証はできません。
そこで、「傾向スコアモデルかアウトカム回帰モデルの少なくとも一方が正しく推定されていれば因果効果の推定結果にバイアスがのらないような推定量」として Doubly robust 推定量が提案されています*8。
処置が二値のとき、処置 の Potential outcome の期待値の Doubly robust 推定量は以下のように定義できます:
\begin{eqnarray}
\hat{\mathbb{E}}_{DR}[Y^{(a')}]
&:=&
\frac{1}{n} \sum_{i=1}^{n}\Bigl[\frac{I(A_i, a')Y_i}{\hat{f}_{A \mid L}(a' \mid L_i)} + \Bigl(1 - \frac{I(A_i, a')}{\hat{f}_{A \mid L}(a' \mid L_i)}\Bigr) \hat{f}_{Y\mid A, L}(a', L_i)\Bigr]
\tag{7}
\end{eqnarray}
what if book では Technical Point 13.2 で紹介されており、 Horvitz-Thompson estimator を アウトカム回帰モデルを伴った関数で補正しているとみなせます:
which can also be viewed as a correction of the Horvitz-Thompson estimator by a function that involves the outcome regression model
式を見ると明らかですが、 summation の中身の一項目は Horvitz-Thompson estimator と同じ形をしています。
また、二項目において、 Standardization を傾向スコアにより補正しています。
要するに、IPW と Standardization の合わせ技が Doubly robust ということになります。
Horvitz-Thompson estimator 以外の IPW 推定量を Doubly robust で使えるか？
さて、IPW を学んできた立場としては、以下のことが気になるのは自然なことかと思います:
- Doubly robust で、 Stabilized weights は使えるのか？
- Doubly robust で、 Horvitz-Thompson estimator 以外の形の推定量も使えるのか？
これについて説明した資料はなかなか見つけられなかったのですが、私の意見は「自明ではなく、難しそう」です。
いくつかの具体例をもとに考察していきます。
例えば、stabilized weights を 式 (7) に導入する方法についていくつか考えてみます。
まず、逆確率の部分を直接処置確率で補正すると、このようになると思います:
\begin{eqnarray}
\frac{1}{n} \sum_{i=1}^{n}\Bigl[\frac{I(A_i, a')\hat{f}_{A}(a')Y_i}{\hat{f}_{A \mid L}(a' \mid L_i)} + \Bigl(1 - \frac{I(A_i, a') \hat{f}_{A}(a') }{\hat{f}_{A \mid L}(a' \mid L_i)}\Bigr) \hat{f}_{Y\mid A, L}(a', L_i)\Bigr]
\tag{8}
\end{eqnarray}
しかしこの式は、「傾向スコアモデルが正しく推定できているがアウトカムモデルが誤って推定されている」ときにバイアスが生じてしまうので、 Doubly robust とは言えません。
また、式全体に対して処置確率で補正をするとこのようになります。
\begin{eqnarray}
\frac{1}{n} \sum_{i=1}^{n}\Bigl[\frac{I(A_i, a')\hat{f}_{A}(a')Y_i}{\hat{f}_{A \mid L}(a' \mid L_i)} + \hat{f}_{A}(a') \Bigl(1 - \frac{I(A_i, a') }{\hat{f}_{A \mid L}(a' \mid L_i)}\Bigr) \hat{f}_{Y\mid A, L}(a', L_i)\Bigr]
\tag{9}
\end{eqnarray}
しかしこの式は、「傾向スコアモデルが誤って推定されているがアウトカムモデルが正しく推定されている」ときにバイアスが生じてしまう上、全体に処置確率をかけているだけなので、 Doubly robust でない上に stabilization の意味もありません。
また、 summation の中身の一項目（Horvitz-Thompson estimator）、あるいは 二項目（Standardization の補正）のどちらか一方にのみ補正を行う場合、色々なケースで明らかにバイアスが出てきてしまうので不適切です。
よって、 Doubly robust で Horvitz-Thompson estimator を扱う場合、 Stabilized weights を使うことは難しいと考えられます。
最後に、Doubly robust で Hajek estimator のようなものを扱う場合を考えてみます。
この記事の前半で述べたように、 Stabilized weights の有用性は Hajek estimator を扱うときに発揮されるので、 Doubly robust でも Hajek estimator のようなものを考えれば Stabilized weights を使えるかもしれないという発想に至るでしょう。
素朴に考えると、以下のように分母をつけたくなるかと思います。
\begin{eqnarray}
\frac{
\sum_{i=1}^{n}\Bigl[\frac{I(A_i, a')Y_i}{\hat{f}_{A \mid L}(a' \mid L_i)} + \Bigl(1 - \frac{I(A_i, a')}{\hat{f}_{A \mid L}(a' \mid L_i)}\Bigr) \hat{f}_{Y\mid A, L}(a', L_i)\Bigr]
}
{
\sum_{i=1}^{n} \Bigl[ \frac{I(A_i, a')}{\hat{f}_{A_i \mid L}(a' \mid L_i)} \Bigr]
}
\tag{10}
\end{eqnarray}
しかし、前回の記事で指摘したように、これは ratio estimator の特殊ケースなので、傾向スコアモデルが正しく推定されていたとしても、不偏性は持たないというのが私の意見です。
またそもそも、傾向スコアモデルが誤って推定されていたとき、分母の期待値は とは大きく異なることが予想されるので、式 (10) は傾向スコアモデルに対してロバストではない（すなわち、 Doubly robust ではない）推定量と言えるかと思います。
よって、 Hajek estimator のような形の Doubly robust 推定量を作ることは難しく、式 (10) に対する stabilized weights を考えるまでもなくお蔵入りになってしまうでしょう。
まとめ
本記事では、 IPW の文脈でよく紹介される stabilized weights という重みづけ方法の特徴と、その注意点をまとめました。
一通り読んでいただいた方には、「なんでもかんでも stabilized weights を使えばいい」というわけではないことがお伝えできたかと思います。
今後は、より一般的な連続値の介入を想定した手法や、実験による主張の検証についての記事を書く予定をしています。
記事を読んでいただいた皆さんの豊かな因果推論ライフに貢献できれば幸いです。
*1:もちろんピコ太郎氏の写真は what if book には載っていません。Avex さんの HP (https://avex.jp/pikotaro/) から借りてきました
*2:ご存知の方は教えていただけると幸いです
*3:Technical Point 12.1 で「この章では Hajek esitmator を推定する」とは書かれていますが、これが stabilized weights を使うにあたっての本質的な前提条件であることに気付いている読者は多くはないと思います・・・
*4:これは先ほどの「pseudo-population の世界において確率変数の意味での exchangeability が成立することが何に使えるのかわからない」という疑問とも関連していて、pseudo-population の世界において確率変数の意味での exchangeability が成立するような stabilized weights を使ったとしても、結局は別の基準（不偏性や漸近分散）をもとに議論するのであれば、pseudo-population における exchangeability とはいったい何なんだろう・・・という気持ちになりました
*5:私も適切な説明はまだ思いついていないです
*6:「不偏」の間違いではなく invariant の意味です
*7:g-formula として what if book の 13章で紹介されています
*8:この記事では議論を簡略化するために「真の関数が得られている」という意味での「正しく推定されている」という条件下での不遍性を考えました。しかし、Doubly robust 推定量の性質を語るときには、モデルが特定されている」という条件下での漸近的な不偏性（これを一致性と呼んでいる文献もある気がします）を持つものとしての議論をすることが多いと思われます。適宜読み替えていただけると幸いです
